You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Please help me
- Thread starter abtia
- Start date
D
Deleted member 4993
Guest
I cannot figure out what you need to prove (and what is given) from your post.
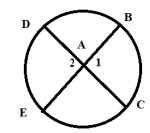
I think you are talking about <1....there is no angle called A1. A is the point where segments DC and BE intersect.
Ok...so you are trying to prove that m<1 = (arc DE + arc BC)/2
Draw segment EC. This will create a triangle EAC, for which <1 is an exterior angle.
You should have a theorem which says that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles (the angles of the triangle which are NOT adjacent to the exterior angle you're working with). In this case, m<1 = m<AEC + m<ACE
Note that we could also refer to <AEC as <BEC, and <ACE as <DCE.
And look! <BEC is an inscribed angle, so its measure is 1/2 of its intercepted arc (which happens to be arc BC). m<AEC = m<BEC = (arc BC)/2
<DCE is also an inscribed angle, so its measure is 1/2 of its intercepted arc (which happens to be arc DE). m<ACE = m<DCE = (arc DE)/2
m<1 = m<AEC + m<ACE, so m<1 = m<BEC + m<DCE
Substitute the expressions we have for m<BEC and m<DCE:
m<1 = (arc BC)/2 + (arc DE)/2
On the right side, we have two fractions with the same denominator. Add the numerators and put the result over the common denominator:
m<1 = (arc BC + arc DE) / 2
That should do it......
Last edited: