vampirewitchreine
Junior Member
- Joined
- Aug 2, 2011
- Messages
- 82
Hi guys, I need a bit of help getting started on this.

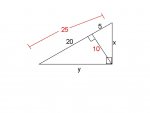
Find the value of each variable.
Extra information: In the big triangle, the altitude does not evenly divide the right angle to a 45 degree on each side (Lets call the big triangle ABC starting from the bottom left and going clockwise. Let's call the altitude segment BD.)

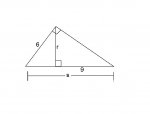
Find the value of each variable.
Extra information: In the big triangle, the altitude does not evenly divide the right angle to a 45 degree on each side (Lets call the big triangle ABC starting from the bottom left and going clockwise. Let's call the altitude segment BD.)