Sin and Cos

[vampirewitchreine]

This is just a check to make sure that I've done this correctly....

Sketch a 45-45-90 triangle and a 30-60-90 triangle. Label each side length. Then use the triangles to find the exact value of each ratio.

24. cos 45°
26. sin 60°
28. cos 30°


My sketch:


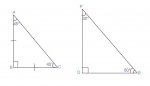
My answers were:
24. .7071
26. .8660
28. .8660

Is this wrong or is this actually okay?

 

[tkhunny]

It is not okay because you were asked to find "exact" values.

\(\displaystyle \cos(45^{\circ}) = \frac{1}{\sqrt{2}}\)

You do the other two. Let's see what you get.

 

[vampirewitchreine]

It is not okay because you were asked to find "exact" values.

\(\displaystyle \cos(45^{\circ}) = \frac{1}{\sqrt{2}}\)

You do the other two. Let's see what you get.

Okay, that makes a lot more sense now...


I've now got:
\(\displaystyle \sin(60^{\circ}) = \frac{1}{2}\)
\(\displaystyle \cos(30^{\circ}) = \frac{1}{2}\)

Correct or no?

 

[tkhunny]

...and thus we see the value of showing your work.

How did you come to those incorrect conclusions? It's particularly curious since your calculator results above do not agree.

 

[vampirewitchreine]

...and thus we see the value of showing your work.

How did you come to those incorrect conclusions? It's particularly curious since your calculator results above do not agree.

I just entered the degree of the angle with the sin and cos keys on the calculator rather than use the formulas that come from the 45-45-90 and 30-60-90 triangles.

 

[tkhunny]

How did you manage a different result from the red versions shown above?

45-45-90 is isosceles. Measures of sides are in the proportions \(\displaystyle 1:1:\sqrt{2}\)

30-60-90 -- Measures of sides, in increasing order, are in the proportions \(\displaystyle 1:\sqrt{3}:2\)

For such triangles, the exact values of sine, cosine, and tangent should be read fluently from this information. It takes practice.

 

[srmichael]

How did you manage a different result from the red versions shown above?

45-45-90 is isosceles. Measures of sides are in the proportions \(\displaystyle 1:1:\sqrt{2}\)

30-60-90 -- Measures of sides, in increasing order, are in the proportions \(\displaystyle 1:\sqrt{3}:2\)

For such triangles, the exact values of sine, cosine, and tangent should be read fluently from this information. It takes practice.

I always tell kids to practice making these two triangles quickly with the ratios on each side as stated above then with good ol' SOHCAHTOA you can easily answer any trig question referring to angles and reference angles of 30, 45 or 60 degrees.

 

[Mrspi]

I always tell kids to practice making these two triangles quickly with the ratios on each side as stated above then with good ol' SOHCAHTOA you can easily answer any trig question referring to angles and reference angles of 30, 45 or 60 degrees.

I always told my students exactly the same thing! I still draw those special triangles myself...even though I'm quite sure I know the trig functions of those special angles by now. I'm happy to hear that someone out there is carrying on the tradition!

 

[vampirewitchreine]

How did you manage a different result from the red versions shown above?

45-45-90 is isosceles. Measures of sides are in the proportions \(\displaystyle 1:1:\sqrt{2}\)

30-60-90 -- Measures of sides, in increasing order, are in the proportions \(\displaystyle 1:\sqrt{3}:2\)

For such triangles, the exact values of sine, cosine, and tangent should be read fluently from this information. It takes practice.

Instead of using the proportions, I used the measure of the angle entered into the sin and cos on my calculator [sin(45), sin (60), cos(30)] and came up with that versus using the actual formulas \(\displaystyle sin= \frac {opposite}{hypotenuse}\) and \(\displaystyle cos= \frac {adjacent}{hypotenuse}\)

 

[Deleted member 4993]

Instead of using the proportions, I used the measure of the angle entered into the sin and cos on my calculator [sin(45), sin (60), cos(30)] and came up with that versus using the actual formulas \(\displaystyle sin= \frac {opposite}{hypotenuse}\) and \(\displaystyle cos= \frac {adjacent}{hypotenuse}\)

Whenever the answer needs to be exact, be wary of using calculators (simple scientific one). Those rarely give you exact value. Unless expressed as fractions, your answers most pobably won't be exact.