vampirewitchreine
Junior Member
- Joined
- Aug 2, 2011
- Messages
- 82
I'm not quite sure which is the correct answer.... because I'm dealing with a square root squared, I have 2 different answers 2 different ways.
Square WXYZ
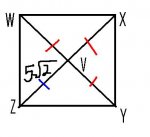
a. WY
b. XY
a.:
I found WY as \(\displaystyle 5\sqrt{2} + 5\sqrt{2}\)
Then\(\displaystyle WY~\approx 7.07 + 7.07\)
Ending with \(\displaystyle WY~\approx 14.14\)
b.:
I found XY in 2 ways, and came up with 2 very different answers. What I'd like to know, is which answer would be correct?
\(\displaystyle XY^2 = XV^2 = YV^2\)
\(\displaystyle XY^2 = 5\sqrt {2}^2 + 5\sqrt {2}^2\) OR \(\displaystyle XY^2 = (5\sqrt {2})^2 + (5\sqrt {2})^2\)
\(\displaystyle XY^2 = 10 + 10\) OR \(\displaystyle XY^2 = 50 + 50\)
\(\displaystyle \sqrt {XY^2} = \sqrt{20}\) OR \(\displaystyle \sqrt {XY^2} = \sqrt {100}\)
\(\displaystyle XY ~\approx 4.47\) OR \(\displaystyle XY = 10 \)
(My feeling is the second one, but I'd like to get your input as well)
Square WXYZ

a. WY
b. XY
a.:
I found WY as \(\displaystyle 5\sqrt{2} + 5\sqrt{2}\)
Then\(\displaystyle WY~\approx 7.07 + 7.07\)
Ending with \(\displaystyle WY~\approx 14.14\)
b.:
I found XY in 2 ways, and came up with 2 very different answers. What I'd like to know, is which answer would be correct?
\(\displaystyle XY^2 = XV^2 = YV^2\)
\(\displaystyle XY^2 = 5\sqrt {2}^2 + 5\sqrt {2}^2\) OR \(\displaystyle XY^2 = (5\sqrt {2})^2 + (5\sqrt {2})^2\)
\(\displaystyle XY^2 = 10 + 10\) OR \(\displaystyle XY^2 = 50 + 50\)
\(\displaystyle \sqrt {XY^2} = \sqrt{20}\) OR \(\displaystyle \sqrt {XY^2} = \sqrt {100}\)
\(\displaystyle XY ~\approx 4.47\) OR \(\displaystyle XY = 10 \)
(My feeling is the second one, but I'd like to get your input as well)














