Finding interior angles of an Irregular Pentagon

[alyxander100]

I have a modeling project I am working on and know what the measurements of the sides of a pentagon need to be, but I don't know what angles I need to draw the lines at so I can cut them from the wood.


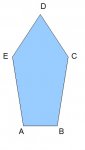
Here is the shape I need the pentagon to have.
Side AB needs to be 1.5"
The interior triangle ABD needs to be 3" in height

I need to know the formulas I need to use to
A: Calculate the angles of each corner
B: Calculate the length of sides AE and BC as well as DE and DC.

The answers would be appreciated as well as the formulas (answers so I can check my work and formulas so I dont have to keep bugging people for the answers later.) I have College Algebra under my belt (154 level) so I am not completely stupid to math...but it has been a while since I have worked with angles and polygons.

Thank you so much for aiding this mathematical infant.
Alyx

 

[alyxander100]

Think I may have it...Check my answer please?

Okay. I think I may have found my answer...I cheated a little, but its a modeling project, so as long as I get the right answer I should be fine.

I started by finding out the info for triangle ABD. I knew that AB was 1.5" and the height of the triangle was 3". I bisected the triangle to find the hypotenuse BD. I found that side BD= 3.1" (Pythagorean Theorem). once I had that, I knew that the bisecting line being 3", BD being 3.1 and knowing the angle of the bisect with AB was a 90 I was able to find that the interior angle of D in triangle ABD was 28 degrees.

I then set out to find the interior angle for D in the pentagon. I saw that CDE formed a perfect Equilateral triangle 2.125" sides and 60 degree angles.

So - Angle D is 60 degrees. and I know the interior angle D from triangle ABD was 28 degrees. So to find the full angle C and B was simple from there. If D is 60 degrees and the D from ABD was 28, to find the angle for triangle BCD, I took 60, subtracted 28 and divided the answer by 2 = 16. So, all of a sudden, I have angle D: 16 degrees, side BD:3.1" and side CD: 2.125". Here is where I cheated - I plugged the info into http://ostermiller.org/calc/triangle.html. and found that angle C is 140 degrees and side BC was 2.5"

That gave me all the info I needed.
Lines:
AB: 1.5"
BC: 2.5"
CD: 2.125"
DE: 2.125"
EA: 2.5"

Angles:
A: 100
B: 100
C: 140
D: 60
E: 140

Is this correct? I know I did it in a rudimentary and roundabout way, but is it correct? also, is there an easier way to do it?

Thanks again!
Alyx

 

[pka]

Okay. I think I may have found my answer...I cheated a little, but its a modeling project, so as long as I get the right answer I should be fine.
View attachment 1688
I started by finding out the info for triangle ABD. I knew that AB was 1.5" and the height of the triangle was 3". I bisected the triangle to find the hypotenuse BD. I found that side BD= 3.1" (Pythagorean Theorem). once I had that, I knew that the bisecting line being 3", BD being 3.1 and knowing the angle of the bisect with AB was a 90 I was able to find that the interior angle of D in triangle ABD was 28 degrees.

I then set out to find the interior angle for D in the pentagon. I saw that CDE formed a perfect Equilateral triangle 2.125" sides and 60 degree angles.

So - Angle D is 60 degrees. and I know the interior angle D from triangle ABD was 28 degrees. So to find the full angle C and B was simple from there. If D is 60 degrees and the D from ABD was 28, to find the angle for triangle BCD, I took 60, subtracted 28 and divided the answer by 2 = 16. So, all of a sudden, I have angle D: 16 degrees, side BD:3.1" and side CD: 2.125". Here is where I cheated - I plugged the info into http://ostermiller.org/calc/triangle.html. and found that angle C is 140 degrees and side BC was 2.5"

That gave me all the info I needed.
Lines:
AB: 1.5"
BC: 2.5"
CD: 2.125"
DE: 2.125"
EA: 2.5"

Angles:
A: 100
B: 100
C: 140
D: 60
E: 140
Is this correct?

If the numbers in blue are correct then those angles are correct.
The add to 540 which is the sum of the interior angles.