You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
chord length
- Thread starter Kenny
- Start date
We're always kind. Why would we be anything else? Thank you.
If you had a semi-circular trough and the water level was constantly changing. You know the depth from the bottom of the trough after the change. How would calculate the chord length in order to find the area? With this I can figure out the volume.
Does that make any sense?
Ken
If you had a semi-circular trough and the water level was constantly changing. You know the depth from the bottom of the trough after the change. How would calculate the chord length in order to find the area? With this I can figure out the volume.
Does that make any sense?
Ken
Last edited:
We're always kind. Why would we be anything else? Thank you.
If you had a semi-circular trough and the water level was constantly changing. You know the depth from the bottom of the trough after the change. How would calculate the chord length in order to find the area? With this I can figure out the volume.
Does that make any sense?
Ken
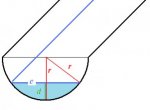
1. Draw a sketch (see attachment)
2. Use the right triangle with the hypotenuse r, the leg (r - d) and the leg \(\displaystyle \tfrac12 c\) to determine the length of c.
Attachments
If the radius = 2’, isn’t the radius and center angle the same in a 180 drgee semicircle?
Ref: http://mathworld.wolfram.com/CircularSegment.html
Ref: http://mathworld.wolfram.com/CircularSegment.html
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
You do not need to know any angles.If the radius = 2’, isn’t the radius and center angle the same in a 180 drgee semicircle?
Ref: http://mathworld.wolfram.com/CircularSegment.html
From formula #9, the cord length is \(\displaystyle 2\sqrt{4d-d^2}\).
At that website \(\displaystyle R=2~\&~h=d\) in your diagram,
You do not need to know any angles.
From formula #9, the cord length is \(\displaystyle 2\sqrt{4d-d^2}\).
At that website \(\displaystyle R=2~\&~h=d\) in your diagram,
Once again thank you. I am not a young man and that old saying "If you don't use it you lose it" is so true. I tried to search for formula #9 just to see what else may be there, the search was in vain. I am a hobbyist and want to incorporate this formula into some code on an MCU, it' a type of microprocessor. If I follow you all I need is the formula from #9 and this is all I need to calculate the area of liquid?
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
I have no idea what you mean by "tried to search for formula #9"Once again thank you. I am not a young man and that old saying "If you don't use it you lose it" is so true. I tried to search for formula #9 just to see what else may be there, the search was in vain. I am a hobbyist and want to incorporate this formula into some code on an MCU, it' a type of microprocessor. If I follow you all I need is the formula from #9 and this is all I need to calculate the area of liquid?
On this page there is a subsection entitled "cord length".
There are four formulae for cord length (6),(7),(8),&(9).
There is formula #9.
Could someone please double check me on this ?
Could any one double check me on this ?
Using pappus drawing: d=12, r=24
Area of a circle-circle =
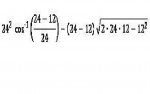
= 192pi-144sqrt(3) = an area of 353.7704731993219
REF: http://mathworld.wolfram.com/Quarter-TankProblem.html
Could any one double check me on this ?
Using pappus drawing: d=12, r=24
Area of a circle-circle =
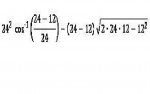
= 192pi-144sqrt(3) = an area of 353.7704731993219
REF: http://mathworld.wolfram.com/Quarter-TankProblem.html
Last edited: