You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
what is the amount of A+B+C+D+E+F+G
- Thread starter abtia
- Start date
D
Deleted member 4993
Guest
Hi,
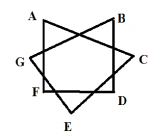
in the following image we want to find the sum of following angles:A+B+C+D+E+F+G
View attachment 1776
You have posted several problems here- i think ~6 of those - without showing one line of work (from you). To get prompt response from us, you must show your work.
Please share your work with us, indicating exactly where you are stuck - so that we may know where to begin to help you.
Last edited by a moderator:
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
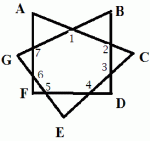 I have numbered the angles in that seven sided convex polygon.The sum of their measures is \(\displaystyle \sum\limits_{k = 1}^7 {m(\angle k) = 900^o } \).Using the external angle theorem we get:\(\displaystyle m(\angle 1) = m(\angle B) + \left( {180^o - m(\angle 2)} \right)\) \(\displaystyle m(\angle 2) = m(\angle C) + \left( {180^o - m(\angle 3)} \right)\)\(\displaystyle m(\angle 3) = m(\angle D) + \left( {180^o - m(\angle 4)} \right)\)\(\displaystyle m(\angle 4) = m(\angle E) + \left( {180^o - m(\angle 5)} \right)\)\(\displaystyle m(\angle 5) = m(\angle F) + \left( {180^o - m(\angle 6)} \right)\)\(\displaystyle m(\angle 6) = m(\angle G) + \left( {180^o - m(\angle 7)} \right)\)\(\displaystyle m(\angle 7) = m(\angle A) + \left( {180^o - m(\angle 1)} \right)\)Now if we add these seven equations we see your professor's answer is correct.
I have numbered the angles in that seven sided convex polygon.The sum of their measures is \(\displaystyle \sum\limits_{k = 1}^7 {m(\angle k) = 900^o } \).Using the external angle theorem we get:\(\displaystyle m(\angle 1) = m(\angle B) + \left( {180^o - m(\angle 2)} \right)\) \(\displaystyle m(\angle 2) = m(\angle C) + \left( {180^o - m(\angle 3)} \right)\)\(\displaystyle m(\angle 3) = m(\angle D) + \left( {180^o - m(\angle 4)} \right)\)\(\displaystyle m(\angle 4) = m(\angle E) + \left( {180^o - m(\angle 5)} \right)\)\(\displaystyle m(\angle 5) = m(\angle F) + \left( {180^o - m(\angle 6)} \right)\)\(\displaystyle m(\angle 6) = m(\angle G) + \left( {180^o - m(\angle 7)} \right)\)\(\displaystyle m(\angle 7) = m(\angle A) + \left( {180^o - m(\angle 1)} \right)\)Now if we add these seven equations we see your professor's answer is correct.
Last edited: