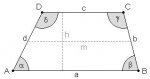
I am back!!! I was so impressed with the information provided to me for the triangle that I think I am ready to attempt the trapezoid I mentioned in the original post of my first thread.
For this problem I will have three inputs: AB, DC, & h (see attached file) and d=b (this will always be equal and will not be an input-it is what it is). Using these inputs, I need to figure out the area of a 1” border all around (just like the triangle example in the above posts). I truly appreciate any help you can provide. Thank you!

For this problem I will have three inputs: AB, DC, & h (see attached file) and d=b (this will always be equal and will not be an input-it is what it is). Using these inputs, I need to figure out the area of a 1” border all around (just like the triangle example in the above posts). I truly appreciate any help you can provide. Thank you!
Attachments
Last edited by a moderator: