You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Find the length of a side?
- Thread starter sacred
- Start date
D
Deleted member 4993
Guest
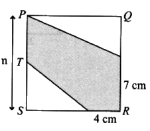
The diagram shows a square with T as the midpoint of PS. Find the perimeter of shaded region in cm. Please show me how to find the length of PS as I was unable to find it.Thanks!

In the absence of any other information, I do not think this problem can be solved.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
The diagram shows a square with T as the midpoint of PS. Find the perimeter of shaded region in cm. Please show me how to find the length of PS as I was unable to find it.
In terms of of \(\displaystyle n\) the area is:
\(\displaystyle n^2-\dfrac{n(n-4)}{4}-\dfrac{n(n-7)}{2}\) WHY$
Last edited:
In the absence of any other information, I do not think this problem can be solved.
Thanks for highlighting, I had the same thought too. Looks like the book had published an invalid question
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
How u do dat, Pka?
Hint: Take away two right triangles.
At first blush, it seems like it should be pretty straightforward. The answer will not be a number, but rather an expression of n Since the figure is a square, each side is the same length. The perimeter of the entire square is, accordingly, 4n. This means that the shaded region must be less than that. Specifically, we just subtract the two legs of each right triangle that are not part of the perimeter of the shaded area. Alternatively, the perimeter of the shaded area will be 11 (the sum of the two known lengths) plus the diagonals of the two right triangles, plus the length of PT.
But something about this just doesn't sit right with me. I've been kind of obsessing all day over this. If we let n = 12, then the first method results in a perimeter of 17cm. But the second method results in a perimeter of 40cm. Surely, if my thought process is correct, then both methods should result in the same number, right?
But something about this just doesn't sit right with me. I've been kind of obsessing all day over this. If we let n = 12, then the first method results in a perimeter of 17cm. But the second method results in a perimeter of 40cm. Surely, if my thought process is correct, then both methods should result in the same number, right?
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
At first blush, it seems like it should be pretty straightforward. The answer will not be a number, but rather an expression of n Since the figure is a square, each side is the same length. The perimeter of the entire square is, accordingly, 4n. This means that the shaded region must be less than that. Specifically, we just subtract the two legs of each right triangle that are not part of the perimeter of the shaded area. Alternatively, the perimeter of the shaded area will be 11 (the sum of the two known lengths) plus the diagonals of the two right triangles, plus the length of PT.
But something about this just doesn't sit right with me. I've been kind of obsessing all day over this. If we let n = 12, then the first method results in a perimeter of 17cm. But the second method results in a perimeter of 40cm. Surely, if my thought process is correct, then both methods should result in the same number, right?
For the sake of good order, THINK!
I gave the area of the shaded part in hopes it would help. Guess not!
Now it is time to play the back-of-the-book game. Look up the answer and figure out WHY?
\(\displaystyle \sqrt{n^2+(n-7)^2}+65+\sqrt{2^{-2}n^2+(n-4)^2}+\dfrac{n}{2}\)
Oh, yeah, I understand now. Sorry for my utter failure - that was certainly embarrassing. Fat lot of good I am as a helper on this website when I've apparently forgotten all my basic geometry skills. All is well though. Smarter minds than myself have proved that this problem is, indeed, solvable, and the world will keep on spinning.
You then need to add the 2 hypotenuses:
13 + 10 = 23; 23 + 17 = 40.
The given answer is indeed 40 cm except I couldn't quite figure out how the length of PS can be derived without having to use the trial method. Please pardon my "mental slowness"