A circle of circumference 12cm is inscribed in a square which in turn is inscribed in an outer circle. This outer circle touches the parallel sides of a trapezium as shown. Find the area of the trapezium, giving your answer in the form (a sqrt(b))/pi
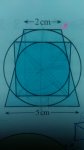
(My first post! Genuinely unsure how to start this question, let alone finish it. Some prompting would be helpful. Also, in case the mathematical form of the answer is confusing, I mean :
a square root b all over pi
Thanks!)

(My first post! Genuinely unsure how to start this question, let alone finish it. Some prompting would be helpful. Also, in case the mathematical form of the answer is confusing, I mean :
a square root b all over pi
Thanks!)
