DanaAJames
New member
- Joined
- Oct 29, 2014
- Messages
- 22
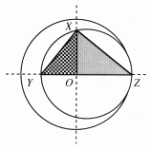
In this diagram, triangleXYZ is inscribed into the circles. O is the center of the larger circle. OZ=x, altitude XO=x-5, and OY=x-9. angleXOZ and angleXOY are both right angles. Using the two similar right triangles OYX, and OXZ, this proportion can be written: OY/OX=OX/OZ
Then: (x-9)/(x-5)= (x-5)/x
I would like to know why this works. How was this proportion written, why it works and how we know triangleOYX is similar to triangleOXZ? I appreciate any information as to why this works.
Then: (x-9)/(x-5)= (x-5)/x
I would like to know why this works. How was this proportion written, why it works and how we know triangleOYX is similar to triangleOXZ? I appreciate any information as to why this works.