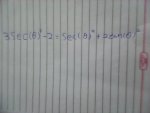You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Can someone help me prove that 3sec(x)^2-2=sec(x)^2+2tan(x)^2 ?
- Thread starter abbb7615
- Start date
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
Use identities for secant and tangent to rewrite each side in terms of cosine and sine.I can't find a way to prove that
Multiply each side by cos(θ)^2.
Does the result give you any ideas? (Hint: There's another identity waiting to be used.) :cool:
D
Deleted member 4993
Guest
In my opinion, a cleaner version would be:Thanks for your answer. I found an easier solution.
3sec(x)² - 2 = sec(x)² + 2tan(x)²
3sec(x)² = sec(x)² + 2( 1 + tan(x)² )
3sec(x)² = sec(x)² + 2sec(x)²
What do you think of this solution ?
3sec²(x) - 2
= sec²(x) + 2sec²(x) - 2
= sec²(x) + 2[sec²(x) - 1]
= sec²(x) + 2[tan²(x)]
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
I think it's great.3sec(x)² - 2 = sec(x)² + 2tan(x)²
3sec(x)² = sec(x)² + 2( 1 + tan(x)² )
3sec(x)² = sec(x)² + 2sec(x)²
What do you think of this solution ?
All three methods in this thread (so far) are solid. :cool: