maxthebat12
New member
- Joined
- Oct 17, 2017
- Messages
- 5
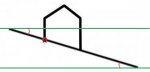
Are you supposed to report A's location using xy-coordinates? If so, are we supposed to assume that the horizontal line segment at the bottom lies on the x-axis and that the Origin is located at its left end?I am struggling on how to find point A on this diagram given to me from my high school teacher.
View attachment 8624
Are you supposed to report A's location using xy-coordinates? If so, are we supposed to assume that the horizontal line segment at the bottom lies on the x-axis and that the Origin is located at its left end?
Well, if your teacher handed you the diagram (with nothing else) and simply said, "Find point A", before walking away, then I would guess that you're free to answer the question in any form that makes sense. Do you agree?
What has your class been studying, lately?
Have you learned about any of the following topics, yet?
Alternate Interior Angles
Similar right triangles
Trigonometry
Slope Formula
Slope-Intercept Form
Point-Slope Form
Yup, but that approach would be my last choice because of extra steps.Is there a way to solve this through trigonometry?
Yup, but that approach would be my last choice because of extra steps.
A more direct approach would be to set up and solve a proportion, based on similar right triangles.
In the diagram below, the green lines are parallel. What can you say about the angles marked in red?
View attachment 8626
Hmmmm....what do "25" and "27" represent?
Yes -- alternate interior angles are always equal, when a transversal crosses a pair of parallel lines.Those angles will always be the same since the lines are parallel?
maxthebat12 has already stated that the uploaded diagram is what they received and that nothing else was provided.Can you post EXACTLY your teacher's original problem?
On second thought, the trigonometric approach is not a lot of extra work; I had failed to consider using the arctangent function (to get the measure of the angle marked in red), when I posted last night.[Trigonometry] would be my last choice …
