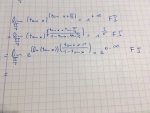e_2.718281828
New member
- Joined
- Feb 11, 2018
- Messages
- 17
I really need help here. (use screenshot pls)
To solve a limit, I always first try to put in the value we're looking at( for this exercise, it's x->Pi/4)
If this gives me an undetermined form, I try to use L'Hopital's rule. However, in this exercise, we do not have a 0/0 or oo/oo solution...
Since we have tan(x + Pi/4) I can use a trigonometric formula that tells me that tan(A + B) = (tan A + tan B)/(1-tan A. tan B)
Still undetermined forms so I use logarithms to make the problem perhaps easier.
f(x)^g(x) = e^(ln(f(x))).g(x), and still nothing. I really hope someone can help me here, it's the last exercise of the series, and I got the first 4 pretty quickly....
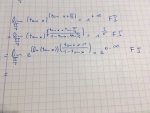
To solve a limit, I always first try to put in the value we're looking at( for this exercise, it's x->Pi/4)
If this gives me an undetermined form, I try to use L'Hopital's rule. However, in this exercise, we do not have a 0/0 or oo/oo solution...
Since we have tan(x + Pi/4) I can use a trigonometric formula that tells me that tan(A + B) = (tan A + tan B)/(1-tan A. tan B)
Still undetermined forms so I use logarithms to make the problem perhaps easier.
f(x)^g(x) = e^(ln(f(x))).g(x), and still nothing. I really hope someone can help me here, it's the last exercise of the series, and I got the first 4 pretty quickly....