I am trying to get my head around thinking about this observation geometrically:
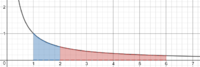
Take f(x) = 1/x and find the area using integration between say x=1 and x= a, lets call that A(a)
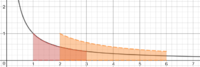
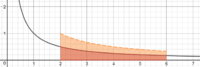
Why is it the case that A(a) + A(b) = A(ab) ?
I can see this comes directly from the properties of logarithms but can't see what is taking place geometrically?
What is about f(x) = 1/x that enables this property to hold? So far my thinking has gone along the lines of stretches and transformations but can't quite put my finger on it.
Is anyone particularly good at thinking geometrically and can offer me some help here?
Take f(x) = 1/x and find the area using integration between say x=1 and x= a, lets call that A(a)
Why is it the case that A(a) + A(b) = A(ab) ?
I can see this comes directly from the properties of logarithms but can't see what is taking place geometrically?
What is about f(x) = 1/x that enables this property to hold? So far my thinking has gone along the lines of stretches and transformations but can't quite put my finger on it.
Is anyone particularly good at thinking geometrically and can offer me some help here?