I am working on a problem involving finding the tangential and normal components of acceleration. This particular problem asks to find the tangential and normal components of acceleration for the function \(r(t)=<\cos(2t),\sin(2t)>\) at \(t=0\) and \(t=1\).
The attached picture is my work. My problem is that my twon components don't change based on the value of t - they are both fixed.
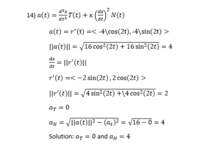
Is this correct? Where am I messing up?
Thank you!
The attached picture is my work. My problem is that my twon components don't change based on the value of t - they are both fixed.
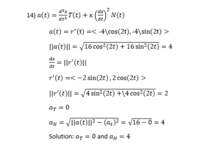
Is this correct? Where am I messing up?
Thank you!
