You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Best way to calculate coordinates?
- Thread starter MathFan
- Start date
Hello, MathFan!
Call that first vertex \(\displaystyle A\).
Label the vertices counterclockwise: \(\displaystyle B,C,D,E.\)
Then we have: .\(\displaystyle \begin{Bmatrix}
A & (5\cos0^o,5\sin0^o) &\approx& (5, 0) \\
B & (5\cos72^o,5\sin72^o) & \approx & (1.545, 4.755) \\
C & (5\cos144^o,5\sin144^o) & \approx & (\text{-}4.045, 2.939)\\
D & (5\cos216^o,5\sin216^o) & \approx & (\text{-}4,045, \text{-}2.939) \\
E & (5\cos288^o,5\sin288^o) & \approx & (1.545, \text{-}4.755)
\end{Bmatrix}\)
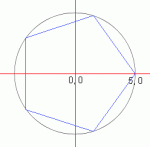
If a regular pentagon is inscribed in a circle,
what is the quickest (most efficient) way to calculate the coordinates
of the vertices given that the centre of the circle is the origin
and one of the vertices is on the positive x-axis?
For example:
View attachment 1615
Call that first vertex \(\displaystyle A\).
Label the vertices counterclockwise: \(\displaystyle B,C,D,E.\)
Then we have: .\(\displaystyle \begin{Bmatrix}
A & (5\cos0^o,5\sin0^o) &\approx& (5, 0) \\
B & (5\cos72^o,5\sin72^o) & \approx & (1.545, 4.755) \\
C & (5\cos144^o,5\sin144^o) & \approx & (\text{-}4.045, 2.939)\\
D & (5\cos216^o,5\sin216^o) & \approx & (\text{-}4,045, \text{-}2.939) \\
E & (5\cos288^o,5\sin288^o) & \approx & (1.545, \text{-}4.755)
\end{Bmatrix}\)
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
This is the same answer given in reply #2. However, if working with a programmable calculator of computer algebra it can be generalized.If a regular pentagon is inscribed in a circle, what is the quickest (most efficient) way to calculate the coordinates of the vertices given that the centre of the circle is the origin and one of the vertices is on the +ve x-axis?
\(\displaystyle \left( {5\cos \left( {\frac{{2k\pi }}{5}} \right),5\sin \left( {\frac{{2k\pi }}{5}} \right)} \right),\;k = 0, \cdots, 4\)
Generalized: if you have a regular N-sided polygon the change 5 to N and 4 to N-1.