vampirewitchreine
Junior Member
- Joined
- Aug 2, 2011
- Messages
- 82
Hi guys,
I'm working on a challenge problem from a previous section(Areas of Regular Polygons and Circles)
Below is the figure that I'm working with:
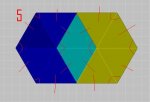
I colored it in different so that it was easier to tell what the figure's edges are. I need to find the area of the shaded region (The diamond shape is the unshaded region, the 2 concave hexagon shapes are the shaded area.....)
Should I solve the diamond shape as a Parallelogram to get the right answer? The height of it should be 5 right?
Correct me if I'm wrong, isn't half the diagonal congruent to one side?
If the above statement is correct:
To find the apothem I have
\(\displaystyle a^2 = 5^2 - 2.5^2\)
\(\displaystyle a^2 = 25 + 6.25 \)
\(\displaystyle \sqrt {a^2} = \sqrt {31.25}\)
\(\displaystyle a ~\approx 5.59 \)
Leaving the area of each hexagons (if you see the diamond shape as where the two overlap)
\(\displaystyle Area = 6(\frac {1}{2}bh)\)
\(\displaystyle Area = 6 (\frac {1}{2} 5 * 5.59)\)
\(\displaystyle Area = 6 (2.5*5.59)\)
\(\displaystyle Area = 6 (13.98) \)
\(\displaystyle Area = 83.85 \)
(This is all that I have so far.... feel free to correct me)
I'm working on a challenge problem from a previous section(Areas of Regular Polygons and Circles)
Below is the figure that I'm working with:

I colored it in different so that it was easier to tell what the figure's edges are. I need to find the area of the shaded region (The diamond shape is the unshaded region, the 2 concave hexagon shapes are the shaded area.....)
Should I solve the diamond shape as a Parallelogram to get the right answer? The height of it should be 5 right?
Correct me if I'm wrong, isn't half the diagonal congruent to one side?
If the above statement is correct:
To find the apothem I have
\(\displaystyle a^2 = 5^2 - 2.5^2\)
\(\displaystyle a^2 = 25 + 6.25 \)
\(\displaystyle \sqrt {a^2} = \sqrt {31.25}\)
\(\displaystyle a ~\approx 5.59 \)
Leaving the area of each hexagons (if you see the diamond shape as where the two overlap)
\(\displaystyle Area = 6(\frac {1}{2}bh)\)
\(\displaystyle Area = 6 (\frac {1}{2} 5 * 5.59)\)
\(\displaystyle Area = 6 (2.5*5.59)\)
\(\displaystyle Area = 6 (13.98) \)
\(\displaystyle Area = 83.85 \)
(This is all that I have so far.... feel free to correct me)
