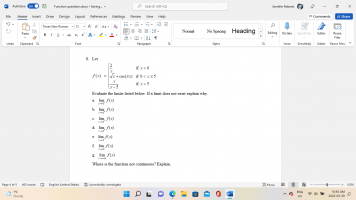
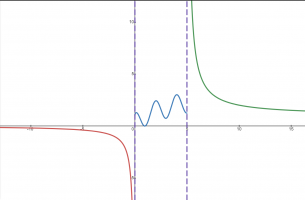
If la-xl is less than delta (and delta is a very small positive number close to zero), then how can f(x) be an unimaginably large number?
That is a really intelligent question.
I am not going to give a formal answer. Instead, I am going to give two informal answers that may be more intuitive.
Consider the function [imath]f(x) = \dfrac{1}{x^4}[/imath]. We want to see what happens as x approaches more closely to zero.
[math]0 < |x| < 10^{-1} = \dfrac{1}{10} \implies 0 < x^4 < \dfrac{1}{10000} \implies \dfrac{1}{x^4} > 10000\\ 0 < |x| < 10^{-2} = \dfrac{1}{100} \implies 0 < x^4 < \dfrac{1}{100,000,000} \implies \dfrac{1}{x^4} > 100,000,000.[/math]
In the second line, x is closer to zero than in the first line, but the minimum possible value of the function is much greater.
More generally, but still not rigorously,
[math]0 < \dfrac{1}{\alpha} < \dfrac{1}{\beta} \implies \alpha > 0 \text { and } \beta > 0 \implies \alpha \beta > 0.\\
\therefore 0 < \dfrac{1}{\alpha} < \dfrac{1}{\beta} \implies \alpha \beta * 0 < \alpha \beta * \dfrac{1}{\alpha} < \alpha \beta * \dfrac{1}{\beta} \implies\\
0 < \beta < \alpha.[/math]
Similarly
[math]\dfrac{1}{\alpha} < \dfrac{1}{\beta} < 0\implies \alpha < 0 \text { and } \beta < 0 \implies \alpha \beta > 0.\\
\therefore \dfrac{1}{\alpha} < \dfrac{1}{\beta} < 0 \implies \alpha \beta * \dfrac{1}{\alpha} < \alpha \beta * \dfrac{1}{\beta} <\alpha \beta * 0 \implies\\
\beta < \alpha < 0.[/math]
The reciprocal of what is closer to zero is farther from zero.
A lot of this limit stuff is a very precise way to state what is intuitively simple.