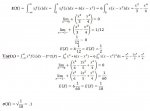Aurelius032
New member
- Joined
- Feb 18, 2015
- Messages
- 6
Find E(X), Var(X) Standard Deviation(X) if a random variable X is given by its density function f(X) such that:
f(x)=0, if x≤0
f(x)=6(x-x^2), if 0<x≤1
f(x)=0, if x>1
My work:
Please see attached.
This is what I have.. I got E(X) = 0 but I do not think this is right. Can anyone check to see if I am doing this wrong? If so, can someone give me hints as to how I can solve this problem?
Also, How do you find VAR(X) and SD(X)??
f(x)=0, if x≤0
f(x)=6(x-x^2), if 0<x≤1
f(x)=0, if x>1
My work:
Please see attached.
This is what I have.. I got E(X) = 0 but I do not think this is right. Can anyone check to see if I am doing this wrong? If so, can someone give me hints as to how I can solve this problem?
Also, How do you find VAR(X) and SD(X)??