Sorry, Let me add a little more information about what I'm trying to do.
In the diagram that I provided, yes R is supposed to represent the unknown radius of the circle that makes up that line, not the length of the curved line.
What I'm doing is trying to come up with a formula that will calculate that changing radius if Y constantly stays the same but x changes in length. This is for a program that will create that curved side according to what value you enter in x.
for example
let's say
y will always equal 152.4
x is a changing value that you're given and are supposed to enter
and the radius (R) is what will be created off those two values
as you make x larger or smaller, essentially stretching that shape, your radius changes along with it.
The previous person that was working on this came up with a formula that supposedly does this, but I'm having trouble deciphering what he's doing.
The following is exactly what he has...
R=(152.4/2)+(X*2)*(X*2)/(8*152.4)
Again, all the information that he was given was just Y=152.4, and X.
In this scenario x=1524... if that helps.
Sorry if I'm not explaining very well. I still assume he's using chord equations because that makes the most sense but I'm totally lost on what he's got going on there.
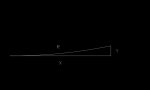
he circle's radius, then you may use the following information, to find the length of the radius.
In the diagram above, S is the segment height, L is half the chord's length, and R is the circle's radius.
If you know any two of these three measurements, you can find the third.
S = R - √[R^2 - L^2]
L = √[2SR - S^2]
R = (S^2 + L^2) / (2S)[/QUOTE]