You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Geometry problem
- Thread starter maine
- Start date
D
Deleted member 4993
Guest
Hello folks, I have serious problems with this task. Anyone have time to help?
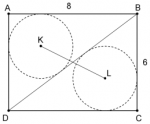
The rectangle ABCD has side lengths AB = 8 og BC = 6.
The inscribed circles in ΔABD and ΔBCD have centers K and L.
Determine the length of the segment KL.
View attachment 1613
The problem can be solved easily using in-center properties discussed in:
http://mathworld.wolfram.com/Incenter.html
Hello, maine!
Consider the right triangle \(\displaystyle ABD.\)
The area of the triangle is: .\(\displaystyle \frac{1}{2}bh \,=\,\frac{1}{2}(6)(8) = 24\)
Using Pythagorus, we find the hypotenuse \(\displaystyle BD = 10.\)
The perimeter of the triangle is: .\(\displaystyle p \:=\:6+8+10 \:=\:24\)
Let \(\displaystyle r\) = radius of the inscribed circle.
The area of the triangle is given by: .\(\displaystyle \text{Area }\:=\: \frac{1}{2}rp\)
Hence, we have: .\(\displaystyle 24 \:=\:\frac{1}{2}r(24) \quad\Rightarrow\quad r = 2\)
Place the rectangle on a coordinate system with vertex \(\displaystyle D\) at the origin.
Then \(\displaystyle K\) is 2 unit to the right and 2 units down from vertex \(\displaystyle A(0,6).\)
. . We have: .\(\displaystyle K(2,4)\)
Similarly, \(\displaystyle L\) is 2 units to the left and 2 units up from vertex \(\displaystyle C(8,0).\)
. . We have: .\(\displaystyle L(6,2)\)
Use the Distance Formula on point \(\displaystyle K\) and \(\displaystyle L.\)
The rectangle ABCD has side lengths AB = 8 and BC = 6.
The inscribed circles in ΔABD and ΔBCD have centers K and L.
Determine the length of the segment KL.
View attachment 1613
Consider the right triangle \(\displaystyle ABD.\)
The area of the triangle is: .\(\displaystyle \frac{1}{2}bh \,=\,\frac{1}{2}(6)(8) = 24\)
Using Pythagorus, we find the hypotenuse \(\displaystyle BD = 10.\)
The perimeter of the triangle is: .\(\displaystyle p \:=\:6+8+10 \:=\:24\)
Let \(\displaystyle r\) = radius of the inscribed circle.
The area of the triangle is given by: .\(\displaystyle \text{Area }\:=\: \frac{1}{2}rp\)
Hence, we have: .\(\displaystyle 24 \:=\:\frac{1}{2}r(24) \quad\Rightarrow\quad r = 2\)
Place the rectangle on a coordinate system with vertex \(\displaystyle D\) at the origin.
Then \(\displaystyle K\) is 2 unit to the right and 2 units down from vertex \(\displaystyle A(0,6).\)
. . We have: .\(\displaystyle K(2,4)\)
Similarly, \(\displaystyle L\) is 2 units to the left and 2 units up from vertex \(\displaystyle C(8,0).\)
. . We have: .\(\displaystyle L(6,2)\)
Use the Distance Formula on point \(\displaystyle K\) and \(\displaystyle L.\)