vampirewitchreine
Junior Member
- Joined
- Aug 2, 2011
- Messages
- 82
In square WXYZ, find the measure of angle WVX, WX and ZV.
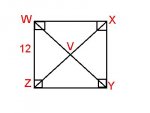
I've got WX as 12 (since it's a square and all sides are congruent)
The measure of angle WVX is 90 [Since the diagonals make the corners all 45 when divided (180-45-45=90).... or the simplified version of the diagonals for perpendicular bisectors]
What I need help with is how to get ZV since ▲WVZ is a right triangle, i've got 2 variables instead of one to work with (Since I would need to know one of the other halves of the diagonals if I use the pre-given information)
Could some one help me to figure out how to solve?

I've got WX as 12 (since it's a square and all sides are congruent)
The measure of angle WVX is 90 [Since the diagonals make the corners all 45 when divided (180-45-45=90).... or the simplified version of the diagonals for perpendicular bisectors]
What I need help with is how to get ZV since ▲WVZ is a right triangle, i've got 2 variables instead of one to work with (Since I would need to know one of the other halves of the diagonals if I use the pre-given information)
Could some one help me to figure out how to solve?
