vampirewitchreine
Junior Member
- Joined
- Aug 2, 2011
- Messages
- 82
(Teal indicates the measurements given by my book, blue is measurements that I figured out)
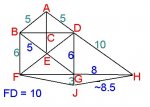
In the diagram, BDGF is a rectangle and FDHJ is a kite.
(I apologize for posting a list, but it makes more sense with my measurements if I post all of the questions)
14. FD=10 (FE+ED=FD)
15. FG=??? (This is where I need help)
16. BE=5 (BE is congruent to BA)
17. ED=5 (ED is congruent to BE)
18. GH=8 (GH2=DH2-DG2; GH2=102-62; GH2=100-36; \(\displaystyle \sqrt{GH^2}=\sqrt{64}\))
19. JH=\(\displaystyle \sqrt{73}~\approx 8.5\) (JH2=JG2+GH2; JH2=32+82;GH2=9+64; \(\displaystyle \sqrt{GH^2}=\sqrt{73}\))

In the diagram, BDGF is a rectangle and FDHJ is a kite.
(I apologize for posting a list, but it makes more sense with my measurements if I post all of the questions)
14. FD=10 (FE+ED=FD)
15. FG=??? (This is where I need help)
16. BE=5 (BE is congruent to BA)
17. ED=5 (ED is congruent to BE)
18. GH=8 (GH2=DH2-DG2; GH2=102-62; GH2=100-36; \(\displaystyle \sqrt{GH^2}=\sqrt{64}\))
19. JH=\(\displaystyle \sqrt{73}~\approx 8.5\) (JH2=JG2+GH2; JH2=32+82;GH2=9+64; \(\displaystyle \sqrt{GH^2}=\sqrt{73}\))
