Hi all,
I am writing a program and I stumbled upon a problem.
In the program I want to know the position on a grid based on the users GPS position with Longitude(-180, 180) and Latitude(-90, 90).
Every cell in the grid is 10x10, so if a user walks 100 meters west he should have moved 10 cells to the left on the grid.
My problem is that the longitude increases much faster near the north and south pole then it does around the equator.
100 meter west in sweden should be 10 cells left and in spain 100 meter should also be 10 cells.
And also I don't want negative grid positions. (longitude and Latitude can be negative)
In my mind the grid would look something like this:
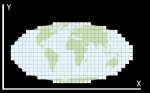
The more north or south you are on the planet the less dense the grid becomes.
I hope this story is clear and that someone can help me out, my head almost explodes at the moment...
I am writing a program and I stumbled upon a problem.
In the program I want to know the position on a grid based on the users GPS position with Longitude(-180, 180) and Latitude(-90, 90).
Every cell in the grid is 10x10, so if a user walks 100 meters west he should have moved 10 cells to the left on the grid.
My problem is that the longitude increases much faster near the north and south pole then it does around the equator.
100 meter west in sweden should be 10 cells left and in spain 100 meter should also be 10 cells.
And also I don't want negative grid positions. (longitude and Latitude can be negative)
In my mind the grid would look something like this:

The more north or south you are on the planet the less dense the grid becomes.
I hope this story is clear and that someone can help me out, my head almost explodes at the moment...
