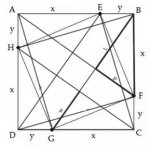
Here is the problem:
Let ABCD be a unit square and mark off points E, F, G, H successively in sides AB, BC,CD,DA so that AE = BF = CG = DH = (2011/2012). Prove that the region that is the intersection of triangles AGB, BHC, CED, DFA is a square with area 1/(2011^2/2012^2).
So I drew out the figure, used sohcahtoa starting with the value (2011/2012). I noticed that the triangle with EA as a hypotenuese is a right triangle, so the angle opposite AE is 90 degrees. With that I figured out the rest of the values, ending up with 2.233 as the value of BG, BH, CH, etc. I subtracted 0.995 and 0.0947 from 2.233, (the values outside the length of "s," the side of the square in question. I got 1.1433, squared that and got 2.0534-ish. Which is definitely not 1/(2011^2/2012^2). Could it be that I just messed up the roundings?
Any help would be greatly appreciated.
P.S. This is an extra credit question for my math class, in case you were wondering why it is so strange.
Let ABCD be a unit square and mark off points E, F, G, H successively in sides AB, BC,CD,DA so that AE = BF = CG = DH = (2011/2012). Prove that the region that is the intersection of triangles AGB, BHC, CED, DFA is a square with area 1/(2011^2/2012^2).
So I drew out the figure, used sohcahtoa starting with the value (2011/2012). I noticed that the triangle with EA as a hypotenuese is a right triangle, so the angle opposite AE is 90 degrees. With that I figured out the rest of the values, ending up with 2.233 as the value of BG, BH, CH, etc. I subtracted 0.995 and 0.0947 from 2.233, (the values outside the length of "s," the side of the square in question. I got 1.1433, squared that and got 2.0534-ish. Which is definitely not 1/(2011^2/2012^2). Could it be that I just messed up the roundings?
Any help would be greatly appreciated.
P.S. This is an extra credit question for my math class, in case you were wondering why it is so strange.