How do I solve this type of problem?
- Thread starter Centurion
- Start date
What do you mean by "solve"? (No equation, no variable, only one real number ... strange!)
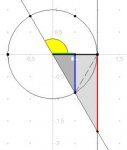
If (and only if) you want to derive the value of \(\displaystyle \tan\left(\frac23 \pi \right)\) then you can use a unit circle, an equilateral triangle and proportions. See attachment.
The blue and green line segments can be calculated using Pythagorean theorem. Afterwards use similar right triangles. The red line segment corresponds to the value of \(\displaystyle \tan\left(\frac23 \pi \right)\). Be aware that the line segments have signs!
EDIT: I apologize, because I posted the wrong image. Now this mistake is repaired.
Attachments
Last edited:
1. The dark grey right triangle is half of a equilateral triangle. Therefore the green line segment has the length \(\displaystyle \tfrac12\) and the blue line segment hast the length \(\displaystyle -\tfrac12 \cdot \sqrt{3}\) (because it is going down!)
2. The light grey right triangles has the legs with lengthes 1 (in black) and \(\displaystyle \tan\left(\tfrac23 \pi \right) = x\) (drawn in red). The light grey triangle and the dark grey triangle are similar. Use proportions:
\(\displaystyle \displaystyle{\frac x1} = \frac{-\tfrac12 \cdot \sqrt{3}}{\tfrac12}}\)
Solve for x.
Last edited: