Ganesh Ujwal
New member
- Joined
- Aug 10, 2014
- Messages
- 32
In the below figure, O is the center of the circle. Radius is 7 cm. [ tex]\angle BOC[ /tex] = 120 Find the length of BC?
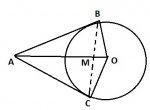
Solution: Join AO to meet BC in M
\(\displaystyle \Delta ABC\) \(\displaystyle \cong\) \(\displaystyle \Delta AOC\) and
\(\displaystyle \Delta BMO\) \(\displaystyle \cong\) \(\displaystyle \Delta CMO\)
\(\displaystyle \angle BMO\) = 90
Triangle BMO has three angles are 90, 60 and 30.
The sides are in the ratio of 2: \(\displaystyle \sqrt 3\) : 1
2X = 7 \(\displaystyle \Rightarrow\) X = 7/2
BM = \(\displaystyle \Rightarrow\) \(\displaystyle \sqrt 3\) x 7 / 2 = 7\(\displaystyle \sqrt 3 / 2\)
BC = 2 x 7\(\displaystyle \sqrt 3 / 2\) = 7 \(\displaystyle \sqrt 3\)

Solution: Join AO to meet BC in M
\(\displaystyle \Delta ABC\) \(\displaystyle \cong\) \(\displaystyle \Delta AOC\) and
\(\displaystyle \Delta BMO\) \(\displaystyle \cong\) \(\displaystyle \Delta CMO\)
\(\displaystyle \angle BMO\) = 90
Triangle BMO has three angles are 90, 60 and 30.
The sides are in the ratio of 2: \(\displaystyle \sqrt 3\) : 1
2X = 7 \(\displaystyle \Rightarrow\) X = 7/2
BM = \(\displaystyle \Rightarrow\) \(\displaystyle \sqrt 3\) x 7 / 2 = 7\(\displaystyle \sqrt 3 / 2\)
BC = 2 x 7\(\displaystyle \sqrt 3 / 2\) = 7 \(\displaystyle \sqrt 3\)
Last edited:
