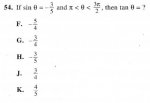You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
If sin θ = (-3/5) and pi < θ < 3pi/2, then what is tan θ?
- Thread starter abplesauc
- Start date
- Joined
- Feb 4, 2004
- Messages
- 16,582
How did you get this as your answer? What was your reasoning? What were your steps?If sin θ = (-3/5) and pi < θ < 3pi/2, then what is tan θ?
I got -3/4, but that is incorrect!
For instance, what did the negative value of the sine tell you about the possible location(s) of the terminal side of the angle, theta? In light of the given restriction on the angle, what did this tell you about the third side (length? sign?) of the triangle drawn in the appropriate quadrant? Taking the appropriate two sides of this triangle for the tangent, how did you arrive at your value?
Please be complete. Thank you!
- Joined
- Apr 12, 2005
- Messages
- 11,339
That's the problem with labeling triangles with negative values. It is easy to become confused.
Think about Quadrant III
cosine is negative
sin is negative
tangent is ??
Don't use negative labels for triangles (or any other real object). Remember where you are!
Think about Quadrant III
cosine is negative
sin is negative
tangent is ??
Don't use negative labels for triangles (or any other real object). Remember where you are!
- Joined
- Feb 4, 2004
- Messages
- 16,582
Okay. Where did you account for the fact that the original sine value was negative? How did you use this information to narrow down the location of the terminal side of the angle?I created a right triangle (using 'SOH CAH TOA') and wrote the side lengths. Using pythagorean theorem, I deduced that the missing side length was 4.
Where did you use the quadrant information that they gave you? How did you draw the reference triangle in the four quadrants? Where did you draw the remaining side, in the x,y-plane?
(Yes, you need to use all of the information, both that they gave you and also that I spelled out for you!)