Ganesh Ujwal
New member
- Joined
- Aug 10, 2014
- Messages
- 32
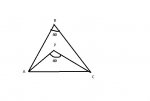
In Triangle ABC, internal bisector of ∠ABC, external bisector of ∠ACB meet at P.
In Triangle ABC, the internal bisector of [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]A[/FONT][FONT=MathJax_Math-italic]B[/FONT][FONT=MathJax_Math-italic]C[/FONT][/FONT] and the external bisector of [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]A[/FONT][FONT=MathJax_Math-italic]C[/FONT][FONT=MathJax_Math-italic]B[/FONT][/FONT] meet at P. If [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]B[/FONT][FONT=MathJax_Math-italic]A[/FONT][FONT=MathJax_Math-italic]C[/FONT][/FONT] = 40 what is the measure of [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]B[/FONT][FONT=MathJax_Math-italic]P[/FONT][FONT=MathJax_Math-italic]C[/FONT][/FONT]?
1) 40
2) 20
3) 70
4) 35
5) None of these.
In Triangle ABC, the internal bisector of [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]A[/FONT][FONT=MathJax_Math-italic]B[/FONT][FONT=MathJax_Math-italic]C[/FONT][/FONT] and the external bisector of [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]A[/FONT][FONT=MathJax_Math-italic]C[/FONT][FONT=MathJax_Math-italic]B[/FONT][/FONT] meet at P. If [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]B[/FONT][FONT=MathJax_Math-italic]A[/FONT][FONT=MathJax_Math-italic]C[/FONT][/FONT] = 40 what is the measure of [FONT=MathJax_Main]∠[FONT=MathJax_Math-italic]B[/FONT][FONT=MathJax_Math-italic]P[/FONT][FONT=MathJax_Math-italic]C[/FONT][/FONT]?
1) 40
2) 20
3) 70
4) 35
5) None of these.