Integral Test

[I Love Pi]

Hi, I am struggling to show that the given series diverges.

 

[BigBeachBanana]

Hi, I am struggling to show that the given series diverges.

Why do you think it diverges? You've shown otherwise, yet you concluded that it diverges?

 

[I Love Pi]

I made the respective corrections. Thank you very much for your help!

 

[BigBeachBanana]

I made the respective corrections. Thank you very much for your help!

One comment about your work.
Note that:
[math]\int_{2}^{\infty}\frac{e^x}{1+e^{2x}}dx\approx0.13452\\ \sum_{n=2}^{\infty}\frac{e^n}{1+e^{2n}}\approx 0.21153[/math]So it's incorrect for you to say this:

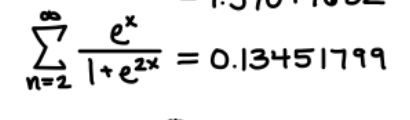
Also, you have both n and x.
It's sufficient to conclude that- By the integral test, since [imath]\int_{2}^{\infty}\frac{e^x}{1+e^{2x}}dx[/imath] converges, so is [imath]\sum_{n=2}^{\infty}\frac{e^n}{1+e^{2n}}[/imath]

 

[Steven G]

I too have some comments on your work.
Do not use equal signs when you have an approximation.
What are the meaning of those check marks you put where it seems that you are justifying that you can use the integral test?
You need to show that a_n is a decreasing sequence! (or do you?)
You need to show that a_n>0 for all n! (or do you?)
You need to show that f(x) is continuous on [2,oo]!
Check marks mean nothing!
Please show us your work for the rest of the problem!

I will show you how I would show that a_n>0 for all n

eⁿ>0 for all n. So the numerator is positive.
e²ⁿ > 0 for all n.
1 + e²ⁿ > e²ⁿ >0 for all n. So the denominator is positive.
....