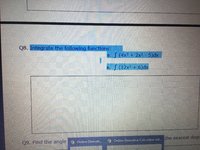
Looking for help please, I'm not sure what the question is asking?

Here is what you do.
If the question were \(\int {(16x^3 + 3x)dx}\) then
the answer would be \(4x^4+\frac{3}{2}x^2\)
because the derivative \(\dfrac{d}{dx}\left(4x^4+\frac{3}{2}x^2\right)=16x^3+3x\)
 
OK so I don't need to give an example after seeing the video above. A quick explanation might lead to a better understanding.

Integration is the reverse process of differentiation. When we differentiate we start with an expression and proceed to find its derivative. When we integrate we start with the derivative and then find the expression from which is has been derived.
 
pka said:
You posted two questions. That is not the answer to either.
So what are you asking about?
Click to expand...
I thought I had to plus the two answers I got together. The answers I got were 8x squared -5x + C and 12x squared - 6x + C
 
pka said:
You posted two questions. That is not the answer to either.
So what are you asking about?
Click to expand...

I thought I had to plus the two answers I got together. The answers I got were 8x squared -5x + C and 12x squared - 6x + C
 
Ciarán said:
I thought I had to plus the two answers I got together. The answers I got were 8x squared -5x + C and 12x squared - 6x + C
Click to expand...
Maybe you'd better post your work. It looks like you are mixing up integration and derivative concepts.

-Dan
 
Ciarán said:
I thought I had to plus the two answers I got together. The answers I got were 8x squared -5x + C and 12x squared - 6x + C
Click to expand...
Can you do derivatives? If so post the answer to these.
\(D_x\left(x^4+\frac{2}{3}x^3-5x \right)=~?\)
\(D_x\left(4x^3+6x \right)=~?\)
While you are learning to do these forget in bogus \(C\).
 
pka said:
Can you do derivatives? If so post the answer to these.
\(D_x\left(x^4+\frac{2}{3}x^3-5x \right)=~?\)
\(D_x\left(4x^3+6x \right)=~?\)
While you are learning to do these forget in bogus \(C\).
Click to expand...

pka said:
Can you do derivatives? If so post the answer to these.
\(D_x\left(x^4+\frac{2}{3}x^3-5x \right)=~?\)
\(D_x\left(4x^3+6x \right)=~?\)
While you are learning to do these
topsquark said:
Maybe you'd better post your work. It looks like you are mixing up integration and derivative concepts.

-Dan
Click to expand...
1588145424607.jpeg
Click to expand...
 
You must log in or register to reply here.
Top