I am reading Math for the Millions and can't do some of the problems in chapter 5.
Both of these problems have answers in the back, so I know what I'm coming up with is wrong. I just don't know why or what I am supposed to be doing.
I'm guessing both problems require the same trick. (That apparently I don't know.)
#12:
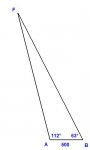
From a base line AB, 500 yards long, the bearings of a flagstaff from A and B are 112 degrees and 63 degrees respectively. Find the distance of the flagstff from A.
answer is 5910.
The wording on this one is a little weird, so I thought I just wasn't understanding it. However, then #13 came along and the wording is very clear on this one, yet I still can't find the right answer.
#13:
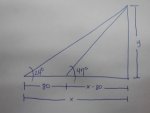
From a boat out at sea the evlation of the top of a cliff is found to be 24 degrees. The boatman rows 80 feet straight towards the cliff, and the elvation of the top of the cliff is now 47 degrees. What is the height of the cliff?
Answer is 60.9 feet
What I need to know is how to get those answers. I am re-reading the chapter and can't figure it out.
Both of these problems have answers in the back, so I know what I'm coming up with is wrong. I just don't know why or what I am supposed to be doing.
I'm guessing both problems require the same trick. (That apparently I don't know.)
#12:
From a base line AB, 500 yards long, the bearings of a flagstaff from A and B are 112 degrees and 63 degrees respectively. Find the distance of the flagstff from A.
answer is 5910.
The wording on this one is a little weird, so I thought I just wasn't understanding it. However, then #13 came along and the wording is very clear on this one, yet I still can't find the right answer.
#13:
From a boat out at sea the evlation of the top of a cliff is found to be 24 degrees. The boatman rows 80 feet straight towards the cliff, and the elvation of the top of the cliff is now 47 degrees. What is the height of the cliff?
Answer is 60.9 feet
What I need to know is how to get those answers. I am re-reading the chapter and can't figure it out.