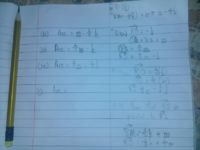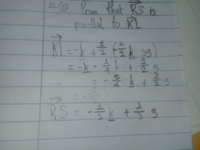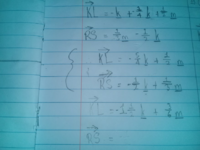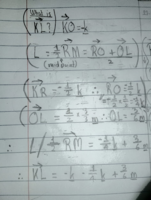You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Need finding my way home! (vectors and matrices)
- Thread starter Denzel
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
I'm not even sure what it means to say a segment (or vector?) is a factor of another, or what RM has to do with a question about RS and KL.So 13. (c) Do I go further or is that it? Should I just say that because RS is a factor of RM therefor it is parallel? Or are there more steps I should take?
I would just write expressions for RS and KL and show that one is a scalar multiple of the other.
It's hard to read your work, but I don't see that you've said anything about KL at all.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
You have expressed the vectors in terms of k and s, by which you apparently mean OS = 1/3 m; they haven't defined that. I used the given k and m instead.
But in RS, you used 1/3 s where you should have had s, or 1/3 m. Your KL also is not quite correct; write out a couple more steps in your work so you can check it more easily.
Make those corrections, and then express all the fractions in each of KL and RS using a common denominator. That will make the fact you need to show clearer.
But in RS, you used 1/3 s where you should have had s, or 1/3 m. Your KL also is not quite correct; write out a couple more steps in your work so you can check it more easily.
Make those corrections, and then express all the fractions in each of KL and RS using a common denominator. That will make the fact you need to show clearer.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
You have
Write each of these using a common denominator, and factor out a fraction to see if they are parallel:
Clearly they are not parallel, if your work is correct, so go back and check. I'd suggest focusing on KL, the more complicated one, and write more steps, as I said before. It appears that you are thinking KL = -OK + OL, and OK = k while OL = -1/4 k + 1/2 m. But what is OL, really?
KL = -5/4 k + 1/2 m
RS = -1/2 k + 1/3 m
Write each of these using a common denominator, and factor out a fraction to see if they are parallel:
KL = -5/4 k + 2/4 m = (1/4)(-5 k + 2 m)
RS = -3/6 k + 2/6 m = (1/6)(-3 k + 2 m)
Clearly they are not parallel, if your work is correct, so go back and check. I'd suggest focusing on KL, the more complicated one, and write more steps, as I said before. It appears that you are thinking KL = -OK + OL, and OK = k while OL = -1/4 k + 1/2 m. But what is OL, really?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
Some crucial parts are too faint to be sure of, but your KL at least is still wrong. (I think RS is right.) You still aren't showing enough steps for me to tell where you are going wrong.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
Some of this makes no sense to me, especially the second line. L is not a vector, and RM is not PO + OL. And your result for KL is just a little off as a result.
Here's how I might start:
Now put in the names k and m appropriately, and see what you get. As I said, because there is a lot going on here, we need to write down the details in a way we can check before going on. (I made a mistake or two in this before getting it right, because I was trying to do it all in my head - not a good idea!)
Here's how I might start:
KL = KO + OL
= KO + OR + RL
= KO + OR + 1/2 RM
= KO + OR + 1/2(RO + OM)
Now put in the names k and m appropriately, and see what you get. As I said, because there is a lot going on here, we need to write down the details in a way we can check before going on. (I made a mistake or two in this before getting it right, because I was trying to do it all in my head - not a good idea!)
I don't understand what OR→ is... or rather, why is it there?Some of this makes no sense to me, especially the second line. L is not a vector, and RM is not PO + OL. And your result for KL is just a little off as a result.
Here's how I might start:
KL = KO + OL= KO + OR + RL= KO + OR + 1/2 RM= KO + OR + 1/2(RO + OM)
Now put in the names k and m appropriately, and see what you get. As I said, because there is a lot going on here, we need to write down the details in a way we can check before going on. (I made a mistake or two in this before getting it right, because I was trying to do it all in my head - not a good idea!)
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
Do you understand now, since you got the correct answer?I don't understand what OR→ is... or rather, why is it there?
We need OR in order to find OL, based on its definition. There may well be several other ways to do this, though.
In your final answer, you should have some parentheses that you omitted, but you did what I did. Both are multiples of -3k + 2m, so they are parallel.
I actually still don't understand the concept behind OR... v_vDo you understand now, since you got the correct answer?
We need OR in order to find OL, based on its definition. There may well be several other ways to do this, though.
In your final answer, you should have some parentheses that you omitted, but you did what I did. Both are multiples of -3k + 2m, so they are parallel.
Last edited:
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
OR is the vector from O to R. What is it that you don't understand?
Is it not clear that OL = OR + RL? (I just noticed that when you copied my work, you wrote OR in place of KO on the first line, which would indeed be confusing if it were what I wrote.)
Is it not clear that OL = OR + RL? (I just noticed that when you copied my work, you wrote OR in place of KO on the first line, which would indeed be confusing if it were what I wrote.)
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
They state right in the problem that OK = k.
The midpoint of segment RM is the point L. Its position vector is OL, and is the average of position vectors OR and OM.
RO + OM is the vector RM; half of that is the vector RL.
I think you may be confusing points and vectors.
The midpoint of segment RM is the point L. Its position vector is OL, and is the average of position vectors OR and OM.
RO + OM is the vector RM; half of that is the vector RL.
I think you may be confusing points and vectors.