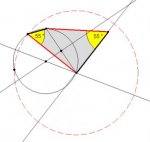
had a student ask this today and I could not give a sufficient answer.
If you know a quadrilateral has ONE pair of opposite congruent sides and ONE pair of opposite congruent angles, why isn't that sufficient to say that it's a parallelogram.
I cannot figure out how I could construct a counterexample that is not a parallelogram.
Help?
If you know a quadrilateral has ONE pair of opposite congruent sides and ONE pair of opposite congruent angles, why isn't that sufficient to say that it's a parallelogram.
I cannot figure out how I could construct a counterexample that is not a parallelogram.
Help?