Please help me

[abtia]

Hello everyone please prove the following question:



A1=(BC+DE)/2

 

[Deleted member 4993]

Hello everyone please prove the following question:



A1=BC+DE/2


View attachment 1517

I cannot figure out what you need to prove (and what is given) from your post.

 

[abtia]

I want to prove this formula:
A1=(DE+BC)/2

For more explanation:the sum of the Arcs(BC+DE) in front of internal angle(A1) divided by 2 is equal by the amount of that angle(A1)

 

[Mrspi]

Hello everyone please prove the following question:



A1=(BC+DE)/2


View attachment 1517

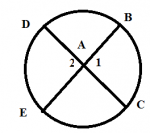
I think you are talking about <1....there is no angle called A1. A is the point where segments DC and BE intersect.

Ok...so you are trying to prove that m<1 = (arc DE + arc BC)/2

Draw segment EC. This will create a triangle EAC, for which <1 is an exterior angle.

You should have a theorem which says that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles (the angles of the triangle which are NOT adjacent to the exterior angle you're working with). In this case, m<1 = m<AEC + m<ACE

Note that we could also refer to <AEC as <BEC, and <ACE as <DCE.
And look! <BEC is an inscribed angle, so its measure is 1/2 of its intercepted arc (which happens to be arc BC). m<AEC = m<BEC = (arc BC)/2

<DCE is also an inscribed angle, so its measure is 1/2 of its intercepted arc (which happens to be arc DE). m<ACE = m<DCE = (arc DE)/2

m<1 = m<AEC + m<ACE, so m<1 = m<BEC + m<DCE
Substitute the expressions we have for m<BEC and m<DCE:
m<1 = (arc BC)/2 + (arc DE)/2

On the right side, we have two fractions with the same denominator. Add the numerators and put the result over the common denominator:

m<1 = (arc BC + arc DE) / 2

That should do it......

 

[abtia]

Thanks a lot my friend....

I am very proud of persons like you: expert and generous.

My problem was solved