You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Please help with this
- Thread starter nathan411
- Start date
D
Deleted member 4993
Guest
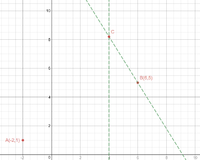
If a line passes through two points - whose co-ordinates are (x1,y1) and (x2,y2) - the equation of the line passing through those points is:A(-2, 1), B(6, 5) and C(4, k) are the vertices of a right- angled triangle ABC.
Angle ABC is the right angle.
Find an equation of the line that passes through A and C.
Give your answer in the form ay + bx + c where a, b and c are integers.
(y - y1)/(x - x1) = (y2 - y1)/(x2 - x1)
Continue....
- Joined
- Nov 24, 2012
- Messages
- 3,021
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
"Find an equation of the line that passes through A(-2,1) and C(4, k).
Give your answer in the form ay + bx + c where a, b and c are integers."
This makes no sense. You are asked to "find an equation" but then told to "give your answer in the form ay+ bx+ c" which is not an equation! I am going to assume that the equation is supposed to be ay+ bx+ c= 0.
At the point A x= -2 and y= 1 so we have a- 2b+ c= 0.
At the point C x= 4 and y= k so we have ka+ 4b+ c= 0.
We have two equations in three unknowns so the solution will not be unique. We can eliminate c by subtracting the first equation from the second: (k-1)a+ 6b= 0. b= (1-k)a/6. Are we to assume that "k" is an integer? If so then so is 1- k and taking a= 6, an integer, b= 1- k, an integer. Putting a= 6, b= 1- k into the equation we got from point A, 6- 2(1- k)+ c= 0 so c= 2- 2k- 6= -4- 2k.
An equation of the line is 6y+ (1-k)x- 4- 2k= 0.
This is a solution. Choosing a to be other non-zero multiples of 6 would give other valid solutions.
Give your answer in the form ay + bx + c where a, b and c are integers."
This makes no sense. You are asked to "find an equation" but then told to "give your answer in the form ay+ bx+ c" which is not an equation! I am going to assume that the equation is supposed to be ay+ bx+ c= 0.
At the point A x= -2 and y= 1 so we have a- 2b+ c= 0.
At the point C x= 4 and y= k so we have ka+ 4b+ c= 0.
We have two equations in three unknowns so the solution will not be unique. We can eliminate c by subtracting the first equation from the second: (k-1)a+ 6b= 0. b= (1-k)a/6. Are we to assume that "k" is an integer? If so then so is 1- k and taking a= 6, an integer, b= 1- k, an integer. Putting a= 6, b= 1- k into the equation we got from point A, 6- 2(1- k)+ c= 0 so c= 2- 2k- 6= -4- 2k.
An equation of the line is 6y+ (1-k)x- 4- 2k= 0.
This is a solution. Choosing a to be other non-zero multiples of 6 would give other valid solutions.
I believe the asker desires an equation with only the variables y and x, not k as well."Find an equation of the line that passes through A(-2,1) and C(4, k).
Give your answer in the form ay + bx + c where a, b and c are integers."
This makes no sense. You are asked to "find an equation" but then told to "give your answer in the form ay+ bx+ c" which is not an equation! I am going to assume that the equation is supposed to be ay+ bx+ c= 0.
At the point A x= -2 and y= 1 so we have a- 2b+ c= 0.
At the point C x= 4 and y= k so we have ka+ 4b+ c= 0.
We have two equations in three unknowns so the solution will not be unique. We can eliminate c by subtracting the first equation from the second: (k-1)a+ 6b= 0. b= (1-k)a/6. Are we to assume that "k" is an integer? If so then so is 1- k and taking a= 6, an integer, b= 1- k, an integer. Putting a= 6, b= 1- k into the equation we got from point A, 6- 2(1- k)+ c= 0 so c= 2- 2k- 6= -4- 2k.
An equation of the line is 6y+ (1-k)x- 4- 2k= 0.
This is a solution. Choosing a to be other non-zero multiples of 6 would give other valid solutions.
D
Deleted member 4993
Guest
MarkFL (response#3) provided the method/process needed to calculate the numerical value of "k".I believe the asker desires an equation with only the variables y and x, not k as well.