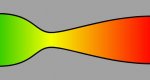
Hi All,
I am working on a problem where I would hope that there is a solution or a general formula for it. I am trying to find a polynomial represents a C-D nozzle as in the following picture. The polynomial must except the length of the C-D nozzle, nozzle radius, diffuser radius, throat radius, as well as the number of points that lay on the polynomial.
Is there any formula for this shape like that for an airfoil shape or do I need to create it from scratch
 ? The polynomial must always fit by either change R1, R2, R, and L or by changing one variable?
? The polynomial must always fit by either change R1, R2, R, and L or by changing one variable?
Many thanks in advance,
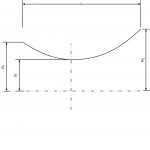
I am working on a problem where I would hope that there is a solution or a general formula for it. I am trying to find a polynomial represents a C-D nozzle as in the following picture. The polynomial must except the length of the C-D nozzle, nozzle radius, diffuser radius, throat radius, as well as the number of points that lay on the polynomial.
Is there any formula for this shape like that for an airfoil shape or do I need to create it from scratch

Many thanks in advance,