Precalculus:Rotation theorem for conics

[skiwilly2001]

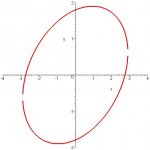
My instructor didn't lecture but just wrote down the theorom and an example. That is all I have to help me. I can get started, but I am getting hung up a the point where you use the half-angle identity. Here is the problem : Find the equation on x y plane and sketch graph. 6x^2-6xy+14y^2-45=0 I know that cot2x=4/3 which means that cos2x=4/5 so I now understand that sinx=+/-sq rt(1-4/5)/2 and I come up with sinx=sq rt 1/10. I don't know where to go from here or if I am even correct to this point. I know the answer is18.4 degrees and (x')^2/9+(y')^2/3=1 and I know the graph. Can anyone help?

 

[BigGlenntheHeavy]

\(\displaystyle A \ reminder: \ With \ all \ conics, \ you \ can \ always \ solve \ explicitly \ for \ y \ or \ x.\)

\(\displaystyle 14y^{2}-6xy+(6x^{2}-45) \ = \ 0\)

\(\displaystyle After \ some \ manipulations, \ we \ get \ y \ = \ \frac{3x \pm \sqrt{630-75x^{2}}}{14}, \ see \ graph.\)

\(\displaystyle We \ would \ have \ a \ normal \ ellipse, \ except \ for \ that \ pesky \ xy \ term.\)

[attachment=0:32kdjvtx]pqr.jpg[/attachment:32kdjvtx]

 

[soroban]

Hello, skiwilly2001!

You say he wrote "the theorem" . . .
Did he give you a list of formulas?

\(\displaystyle \text{Find the equation on the x-y plane and sketch graph: }\;\;6x^2\,-\,6xy\,+\,14y^2\,-\,45\:=\:0\) .[1]

\(\displaystyle \text{I know that: }\cot2x \,=\, \tfrac{4}{3}\;\hdots\;\text{ which means that: }\cos2x \,=\, \tfrac{4}{5}\)

\(\displaystyle \text{So I now understand that: }\sin x \,=\, \pm\tfrac{1}{\sqrt{10}}\)

\(\displaystyle \text{I know the answer is: }18.4^o\;\text{ and }\;\frac{(x')^2}{9} + \frac{(y')^2}{3} \:=\:1\;\;\hdots\text{ and I know the graph.}\)

Can anyone help?

You should have been shown the following before assigning this problem.


\(\displaystyle \text{Given: }\:Ax^2 + Bxy + Cy^2 + Dx + Ey + F \;=\;0\)

\(\displaystyle \text{The angle of rotation }\theta\text{ is given by: }\:\tan2\theta \:=\:\frac{B}{A-C}\)

\(\displaystyle \text{The "new" coordinates are: }\:\begin{Bmatrix}x' &=& x\cos\theta - y\sin\theta \\ y' &=& x\sin\theta + y\cos\theta \end{Bmatrix}\)


\(\displaystyle \text{Discriminant: }\:d \:=\:B^2 - 4AC\)

. . . . \(\displaystyle \begin{array}{ccccc}\text{If } d < 0: & \text{ellipse} \\ \text{If }d = 0: & \text{parabola} \\ \text{If }d > 0: & \text{hyperbola} \end{array}\)


~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~


\(\displaystyle \text{We are given: }\:A = 6,\;B = -6,\;C = 14\)


\(\displaystyle \text{We have: }\:\tan2\theta \:=\:\frac{-6}{8-14} \:=\:\frac{3}{4}\)

\(\displaystyle \text{Then: }\:2\theta \:=\:\arctan(0.75) \:=\:36.86989765^o \quad\Rightarrow\quad\boxed{ \theta \:\approx\:18.4^o}\)

. . \(\displaystyle \text{Also: }\:\begin{Bmatrix}\sin\theta &=& \frac{1}{\sqrt{10}} \\ \\[-3mm] \cos\theta &=& \frac{3}{\sqrt{10}} \end{Bmatrix}\)


\(\displaystyle \text{Hence: }\;\begin{Bmatrix}x' &=& \frac{3}{\sqrt{10}}x - \frac{1}{\sqrt{10}}y &=& \frac{1}{\sqrt{10}}(3x - y) \\ \\[-3mm] y' &=& \frac{1}{\sqrt{10}}x + \frac{3}{\sqrt{10}}y &=& \frac{1}{\sqrt{10}}(x + 3y) \end{Bmatrix}\)


Substitute into [1]:

\(\displaystyle 6\bigg[\frac{1}{\sqrt{10}}(3x-y)\bigg]^2 - \;6\bigg[\frac{1}{\sqrt{10}}(3x-y)\bigg]\,\bigg[\frac{3}{\sqrt{10}}(x + 3y)\bigg] + \;14\bigg[\frac{3}{\sqrt{10}}(x + 3y)\bigg]^2 - \;45 \;=\;0\)

. . . . . . . . . . . . . .\(\displaystyle \frac{6}{10}(3x-y)^2 - \frac{6}{10}(3x-y)(x+3y) + \frac{14}{10}(x+3y)^2 - 45 \;=\;0\)


\(\displaystyle \text{Multiply by 5 and expand: }\;\)

. . . . . \(\displaystyle 3(9x^2 - 6xy + y^2) - 3(3x^2 + 8xy - 3y^2) + 7(x^2 + 6xy + 9y^2) - 225 \;=\;0\)

. . . . . .\(\displaystyle 27x^2 - 18xy + 3y^2 - 9x^2 - 24xy + 9y^2 + 7x^2 + 42xy + 63y^2 - 225 \;=\;0\)


. . \(\displaystyle \text{which simplifies to: }\;25x^2 + 75y^2 \:=\:225\)


\(\displaystyle \text{Divide by 225: }\;\boxed{\frac{x^2}{9} + \frac{y^2}{3} \;=\;1}\)