Hey guys, I have trouble understanding how to know if 2 events are independant or dependant.
For example, if P(A∪B)=0.95 ; P(A)=0.45 ; P(B)=0.5
Based on: P(A∪B)= P(A)+P(B) These would appear to be 2 independent events, with A∩B=Ø
However, what if we decide to draw a Venn diagram that looks like this?
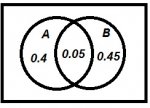
For example, if P(A∪B)=0.95 ; P(A)=0.45 ; P(B)=0.5
Based on: P(A∪B)= P(A)+P(B) These would appear to be 2 independent events, with A∩B=Ø
However, what if we decide to draw a Venn diagram that looks like this?

Last edited:
