Scratching my head
- Thread starter dwpsco
- Start date
How about this?
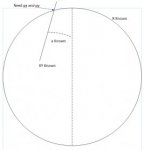
A point (a) within the circle has coordinates (xa, ya). The line segment AP forms an angle @ with a line parallel to the positive y axis. The point of intersection of the line with the circle, P, has coordinates (xp, yp)
I know the Radius of the Circle
I know the xa and xa
I know the @ (theta)
What is the Xp and Yp?
*
* | *
* | P (xp, yp)
* | / *
* | / *
* | | / *
* | | / *
* | |@/ *
* | |/ *
* | a (xa, ya) *
* | *
* | *
----*--------------------+-------------------*------
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
*
A point (a) within the circle has coordinates (xa, ya). The line segment AP forms an angle @ with a line parallel to the positive y axis. The point of intersection of the line with the circle, P, has coordinates (xp, yp)
I know the Radius of the Circle
I know the xa and xa
I know the @ (theta)
What is the Xp and Yp?
*
* | *
* | P (xp, yp)
* | / *
* | / *
* | | / *
* | | / *
* | |@/ *
* | |/ *
* | a (xa, ya) *
* | *
* | *
----*--------------------+-------------------*------
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
* | *
*
Seems to me, you could move the circle around, but R, (x,y), and the angle would remain the same. So maybe it's not possible to find "the" point (px, py)...?
Don't EVER Say that! LOL
Okay the XY of the center of the circle is fixed.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
If you are already scratching, wait until you read this.
House-keeping: Place that diagram on an xy-axis so that (0,0) is the center of the circle.
Let \(\displaystyle Q\) be the known point and the point \(\displaystyle P\) be the unknown point on the circle.
Now the equation of the circle is \(\displaystyle x^2+y^2=r^2\).
Now here is the key to the solution. The slope of the line \(\displaystyle \overleftrightarrow {QP}\) is \(\displaystyle \tan \left( {\frac{\pi }{2} - \alpha } \right)\). To see that think about the definition of slope of a line in terms of the tangent function.
We have a point and a slope, so write the equation of the line.
Find the intersection of the line and the circle.
PLEASE! Do not post your question more than once
http://www.freemathhelp.com/forum/threads/91791-Scratching-my-head
It makes some of us (and me in particular) disinclined to help. I have now erased what I had posted before as it is essentially the same kind of hint given in your other post.
Last edited:
Everything's confused...we're not sure what you're asking...
you don't seem to know yourself what you're doing...
DEAL:
Take some graph paper, draw a circle radius = 8,
center the circle at origin (as Pka suggested).
So the circle's equation is: x^2 + y^2 = 64
From point Q(6,2) inside circle, draw line QP
(P on circle circumference), then extend this
line to meet the y-axis at point A, such that
the angle created at y-axis is 30 degrees.
Can you now calculate the coordinates of point P?
If not, then kiss your problem good-bye and
talk to your teacher.
Well it's true I don't know what i'm doing or I wouldn't be here
To be more clear on the problem, first off I'm 49 yrs old so my teachers are ancient history, so I'm came here to learn. I am building a boat to retire on and cruise about the watery part of the world, and am trying to build the frames, or at least calculate what shape the should be so I CAN build the frames LOL I've created a spreadsheet that calculates most every point of the frames, I've done polynomials for the major curves of the boat, the rest is simple trig.
On the Deck there is a structure called the trunk, it's like a short vertical extension of the deck to give me more head room. So from the outside of the hull, I go inboard 20" and vertically up 1". I know the XY of the outer hull due to the polynomials mentioned above, and so can calculate the Q of the starting point of the trunk. From there I need to angle in 2º and and extend a line to the trunk deck, a developed surface. In the boat building world a developed surface is a surface in the shape of a cone or cylinder since steel don't take compound curves very well. I know the radius of the truck deck at each location I'm trying to find P. I can draw out each and every frame location to find P but it's a bit of work and not very dynamic when I change something, and I would like to enter a formula in to excel so that it is dynamic.
So was hoping for some help, Excel format would be helpful but I do pretty well getting written formulas to work in Excel.
My apologies for posting the first part more then once, I didn't realize you monitor the posts and approve them before they show up, I just figured I was doing something wrong
Well thanks anyways,
A) "Well, this site is mainly to help math students." - Were all students. But yes I get your point.
B) "Looks like Pka, our Resident Boat Expert, has given you what you need... did you read his post" - I read it.
C) Pka didn't help much
D) "I read your last post and understand only .000099% of it" - I guess I didn't Explain myself well enough, sorry my bad.
E) http://mathforum.org/ Math Dr answered my question without all the pomp and pedantic verbiage. Oh and for doing so I donated $200 to their site.
F) ... Ending on "F" seems about right.
Please remove my account I certainly won't be needing it.
Seems to me, you could move the circle around, but R, (x,y), and the angle would remain the same. So maybe it's not possible to find "the" point (px, py)...?
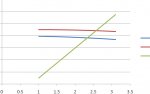
Green line is x = 1 + 5 (y-1), i.e. Point A is (1,1) and the angle is arctan(5).
Blue and red lines are parts of circles with radius eight and centers (0,0) and (1,1) respectively. Point A is certainly inside both circles.
Point P is approximately (8.845, 2.569) for red and (7.653, 2.331) for blue. Seems as though the image won't post as a copy of an image from Word had to save as jpg and upload
Last edited: