Hello all, first time poster.
I am apart of another forum that has challenges. Mostly for web security, but the have programming challenges too which are the ones I like.
Anyway, one of the programming challenges is as fallows:
Given the the figure above is indeed a cube (that is, length, width, and height are all equivalent), and also that the cube is a solid object (that is, you can not go through the cube to get from point 0 to point 1), you must find the shortest distance from point 0 to point 1, moving around the cube.
Example, side length -> 3, answers is 6.
Values given (Length/Height/Width) 4090.6
Figure:
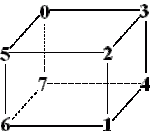
I am not really a math person, more algebra then geometry. I've googled and tried various formulas like:
A) (sqrt(2)*sideLenght)+sideLenght
B) sideLen^2+sideLen^2=c^2
__sideLen^2+c^2 = finalAnswer^2
C) sideLen*root(3)
None of these have worked, even with the proper rounding. I think the formulas I've tried are going through the cube instead of around.
I feel kinda dumb not knowing this, since i did take Geom in highschool, and it's been puzzling me.
Any suggestions?
I am apart of another forum that has challenges. Mostly for web security, but the have programming challenges too which are the ones I like.
Anyway, one of the programming challenges is as fallows:
Given the the figure above is indeed a cube (that is, length, width, and height are all equivalent), and also that the cube is a solid object (that is, you can not go through the cube to get from point 0 to point 1), you must find the shortest distance from point 0 to point 1, moving around the cube.
Example, side length -> 3, answers is 6.
Values given (Length/Height/Width) 4090.6
Figure:

I am not really a math person, more algebra then geometry. I've googled and tried various formulas like:
A) (sqrt(2)*sideLenght)+sideLenght
B) sideLen^2+sideLen^2=c^2
__sideLen^2+c^2 = finalAnswer^2
C) sideLen*root(3)
None of these have worked, even with the proper rounding. I think the formulas I've tried are going through the cube instead of around.
I feel kinda dumb not knowing this, since i did take Geom in highschool, and it's been puzzling me.
Any suggestions?
