trampolinerist
New member
- Joined
- Oct 29, 2017
- Messages
- 4
Hello again,
I am working through an old maths text book for fun and some of my answers don't agree with the book. Please can somebody check my working?
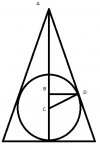
This question says A sphere whose radius is 5cm fits inside a hollow cone so that the top of the sphere is 18cm from the vertex of the cone. find the radius of the circle where the cone touches the sphere.
I drew the rough diagram of a cut away and deduced that the angle at D of triangle ACD should be a right angle as the edge of the cone will be a tangent to the sphere.
We know that CD is 5 cm (the radius of the circle) and that AC is 23cm (The radius 5cm + 18cm to the vertex of the cone).
Therefore AD can be found:-
AD squared + 5 squared = 23 squared
AD = square root of (529 - 25)
AD = square root of (504)
AD = (square root of (36)) * (square root of (14))
AD = 6 * (square root of (14))
Next I deduced that triangle BCD is similar to traingle ACD as they both have a right angle and share the angle at C.
Therefore the ratios:-
BD:CD = AD:AC
BD:5 = (6 * square root of (14))x:23x
5 = 23x
x = 5/23
BD = (6 * square root of (14)) * (5/23)
= (30 x square root of (14))/23
= 4.88cm (3 s.f.)
Thanks in advance for any help.
I am working through an old maths text book for fun and some of my answers don't agree with the book. Please can somebody check my working?
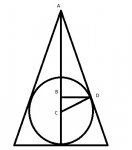
This question says A sphere whose radius is 5cm fits inside a hollow cone so that the top of the sphere is 18cm from the vertex of the cone. find the radius of the circle where the cone touches the sphere.
I drew the rough diagram of a cut away and deduced that the angle at D of triangle ACD should be a right angle as the edge of the cone will be a tangent to the sphere.

We know that CD is 5 cm (the radius of the circle) and that AC is 23cm (The radius 5cm + 18cm to the vertex of the cone).
Therefore AD can be found:-
AD squared + 5 squared = 23 squared
AD = square root of (529 - 25)
AD = square root of (504)
AD = (square root of (36)) * (square root of (14))
AD = 6 * (square root of (14))
Next I deduced that triangle BCD is similar to traingle ACD as they both have a right angle and share the angle at C.
Therefore the ratios:-
BD:CD = AD:AC
BD:5 = (6 * square root of (14))x:23x
5 = 23x
x = 5/23
BD = (6 * square root of (14)) * (5/23)
= (30 x square root of (14))/23
= 4.88cm (3 s.f.)
Thanks in advance for any help.