Stuck on a seeming simple geometry problem

[brutfood]

Stuck on a seemingly simple geometry problem

I'm working on a program, and stuck on something that's reduced nicely to this 2D geometry problem.


I have a line with a known length (d) free to rotate around the origin. Perpandicular to the end of that line is another line that passes through a known point (tx, ty). What is the angle theta ?

 

[Deleted member 4993]

I'm working on a program, and stuck on something that's reduced nicely to this 2D geometry problem.

View attachment 8885
I have a line with a known length (d) free to rotate around the origin. Perpandicular to the end of that line is another line that passes through a known point (tx, ty). What is the angle theta ?

Please share your work with us ...even if you know it is wrong.

If you are stuck at the beginning tell us and we'll start with the definitions.

You need to read the rules of this forum. Please read the post titled "Read before Posting" at the following URL:

http://www.freemathhelp.com/forum/announcement.php?f=33

 

[brutfood]

You need to read the rules of this forum.

Not sure which rule I've broken. The mods can delete this thread if they like.

Anyway - I worked it out in the end. I needed to treat it as lines through the point (tx,ty) that touch the circle (radius-d) tangentially. If I can work out the tangential points on that circle - then I can work out the angle I want. I was stuck before because I was hoping for a simpler geometric trick.

It turns out that when I wrote out the equations of the circle, tangential lines, and normals - and solved/substituted for points on the circle - it boiled down to a quadratic equation.

var a:Number = tx * tx + ty * ty;
var b:Number = - 2 * radius * radius * tx;
var c:Number = radius * radius * radius * radius - radius * radius * ty * ty;

var x0:Number = (-b + Math.sqrt(b * b - 4 * a * c)) / (2 * a);
var y0:Number = (radius * radius - tx * x0) / ty;

var x1:Number = (-b - Math.sqrt(b * b - 4 * a * c)) / (2 * a);
var y1:Number = (radius * radius - tx * x1) / ty;

Anyway - If you're curious what this mathematics is for... I'm working on Inverse Kinematics for robotics. My hobby project. I needed this bit of maths for a heuristic that helps me align shoulder joints on such a way that the rest of the arm is moving in the same plane as the target point.

 

[Dr.Peterson]

I'm working on a program, and stuck on something that's reduced nicely to this 2D geometry problem.

View attachment 8885
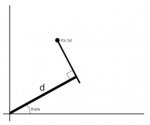
I have a line with a known length (d) free to rotate around the origin. Perpandicular to the end of that line is another line that passes through a known point (tx, ty). What is the angle theta ?

I presume you are aware that there will be two solutions, depending on the orientation of the right angle.

I can think of two entirely different ways to do this immediately, and there are probably a lot more. Which is best may depend on the details you've left out.

One is to use the fact that the right angle is inscribed in a circle whose diameter is the segment joining the origin to the fixed point, so that the triangle formed by its center and the segment of length d is isosceles. That allows you to find the base angles, and then use those to find theta.

Another is to find the coordinates of the right angle in terms of d and theta, and use that to find the coordinates of the given point in terms of c, d, and theta, where c is the length of the perpendicular leg. This gives you two equations in c, d, and theta; you can eliminate c to get a relation between d and theta. Solve this for theta.

I'm not sure which of these will result in a nicer formula -- or something else entirely. What thoughts have you had?