You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
surface area
- Thread starter mathe25
- Start date
Hello, mathe25!
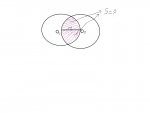
Since \(\displaystyle PQ = P\!A = AQ = r\), triangle \(\displaystyle P\!AQ\) is equilateral.
. . Hence: \(\displaystyle \angle P = \angle Q = \angle A = 60^o\)
In the upper half of the shaded region, we have a sector and a segment.
. . The area of the sector is: .\(\displaystyle \frac{1}{6}\pi r^2\)
. . The area of the segment is:. \(\displaystyle \frac{1}{6}\pi r^2 - \frac{\sqrt{3}}{4}r^2\)
Hence, its area is: .\(\displaystyle \frac{1}{3}\pi r^2 - \frac{\sqrt{3}}{4}r^2\)
Therefore, the shaded region has area:
.. \(\displaystyle 2\times\left(\frac{1}{3}\pi r^2 - \frac{\sqrt{3}}{4}r^2\right) \;=\; \frac{1}{6}\left(4\pi - 3\sqrt{3}\right)r^2 \)
I have two circles and I have only the radius \(\displaystyle r.\)
I must find S, the area of the shaded region.
Code:* * * A * * * * *o* * * *:/:::* * * *:/:::::* * :/::::::: * */::::::::* * * P o:-:-:-:-:o Q * * *:::::::::* - - - - * :::::::::: * *:::::::* * * *:::::* * * *:* * * * * * * *
Since \(\displaystyle PQ = P\!A = AQ = r\), triangle \(\displaystyle P\!AQ\) is equilateral.
. . Hence: \(\displaystyle \angle P = \angle Q = \angle A = 60^o\)
In the upper half of the shaded region, we have a sector and a segment.
. . The area of the sector is: .\(\displaystyle \frac{1}{6}\pi r^2\)
. . The area of the segment is:. \(\displaystyle \frac{1}{6}\pi r^2 - \frac{\sqrt{3}}{4}r^2\)
Hence, its area is: .\(\displaystyle \frac{1}{3}\pi r^2 - \frac{\sqrt{3}}{4}r^2\)
Therefore, the shaded region has area:
.. \(\displaystyle 2\times\left(\frac{1}{3}\pi r^2 - \frac{\sqrt{3}}{4}r^2\right) \;=\; \frac{1}{6}\left(4\pi - 3\sqrt{3}\right)r^2 \)