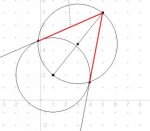
OK so my question is 'Show the lengths of the tangents from the point, P, (5,7) to the circle x2+y2-2x-4y-4=0
And this is how far I've got
[x2-2x+(-1)2]+[y2-4y+(-2)2=4+(-1)2+(-2)2
(x-1)2+(y-2)2=9
Center = (1,2) and Radius = 3
A is the point of contact of one of the tangents, so PA is the length of the tangent and CA is the radius.
CP2=(1+5)2+(2+7)2=117
CAP=90 degrees so PA2=CP2-CA2
PA2=117-9=108
Is all of that right so far? because I feel like some of it is wrong when I start to use Pythagoras.
And this is how far I've got
[x2-2x+(-1)2]+[y2-4y+(-2)2=4+(-1)2+(-2)2
(x-1)2+(y-2)2=9
Center = (1,2) and Radius = 3
A is the point of contact of one of the tangents, so PA is the length of the tangent and CA is the radius.
CP2=(1+5)2+(2+7)2=117
CAP=90 degrees so PA2=CP2-CA2
PA2=117-9=108
Is all of that right so far? because I feel like some of it is wrong when I start to use Pythagoras.