astrophysicsmath
New member
- Joined
- May 1, 2016
- Messages
- 1
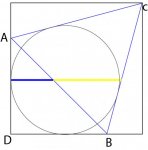
I believe that I have found the golden ratio in the below figure. Geogebra is saying it is very close. Might anyone have a geometric/trigonometric proof?

An equilateral triangle ABC is inscribed in a square so that segment AD is equal to segment DB. A circle is then inscribed so that it is tangent to two sides of the square and two sides of the triangle ABC, as drawn above. Show that the ratio of the yellow segment of the line to the blue segment of the line ( the line which passes through the center of the circle and is perpendicular to the left side of the square while touching the triangle with its other end), is the golden ratio 1.618/1.
An equilateral triangle ABC is inscribed in a square so that segment AD is equal to segment DB. A circle is then inscribed so that it is tangent to two sides of the square and two sides of the triangle ABC, as drawn above. Show that the ratio of the yellow segment of the line to the blue segment of the line ( the line which passes through the center of the circle and is perpendicular to the left side of the square while touching the triangle with its other end), is the golden ratio 1.618/1.