TRIG PROBLEMS. NEED HELP ASAP

[sophia_xo]

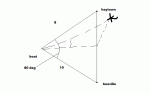
Hey so we just finished our trig unit.. I did AWFUL!! I'm usually in the high 80's in math & I got 65 and its all thanks to these CRAP word problems!! I get everything.. cosine law, sine law, ratios, reciprocal ratios.. I just don't get WORD PROBLEMS & how you draw diagrams.. when they tell you the angle is 30 degrees with the horizontal, WHAT DOES THAT MEAN?? LOL sorry I'm freaking out a bit but yeah..Now we have a make up assignment & I am once again completely lost as to what they're talking about :|.. if some of you guys can do the questions for me or at least draw me the proper diagrams you would honestly MAKE MY DAY...MY WEEK..NO SERIOUSLY PROBABLY MY MONTH.. THANKS SO MUCH!! :

http://i39.tinypic.com/1g0k28.jpg

BTW for number 4, I got that AB is bigger than AC, is that possible? thank youu )

 

[galactus]

#4:

yes, it is possible. AB is longer than AC. The diagram is not to scale.

\(\displaystyle DC=100csc(15)=386.37, \;\ BC=100cot(15)=373.21, \;\ BA=100cot(10)=567.13\)

\(\displaystyle CA=\sqrt{(567.13)^{2}+(373.21)^{2}-2(567.13)(373.21)cos(70)}=562.26\)

Thus, the total distance from D to C to A is 386.37+562.26=948.63

Since he runs at 5 m/s, it takes him 948.63/5=189.73 seconds

For Leanna, at 1 m/s for 100 m it takes her 100 seconds.

But here she runs at 5 m/s. So, it takes her 567.13/5=113.43 seconds plus 100 seconds = 213.43 seconds.

This problem gave the diagram. That was nice.

BTW, an angle to the horizontal is just what it says. It is measured off the horizontal. Like the 10 and 15 degree angles in the diagram for this problem. If it were taken off the vertical, then it would be just that. Taken from a line that is straight up instead of lying down.

 

[sophia_xo]

#4:

yes, it is possible. AB is longer than AC. The diagram is not to scale.

\(\displaystyle DC=100csc(15)=386.37, \;\ BC=100cot(15)=373.21, \;\ BA=100cot(10)=567.13\)

\(\displaystyle CA=\sqrt{(567.13)^{2}+(373.21)^{2}-2(567.13)(373.21)cos(70)}=562.26\)

Thus, the total distance from D to C to A is 386.37+562.26=948.63

Since he runs at 5 m/s, it takes him 948.63/5=189.73 seconds

For Leanna, at 1 m/s for 100 m it takes her 100 seconds.

But here she runs at 5 m/s. So, it takes her 567.13/5=113.43 seconds plus 100 seconds = 213.43 seconds.

This problem gave the diagram. That was nice.

BTW, an angle to the horizontal is just what it says. It is measured off the horizontal. Like the 10 and 15 degree angles in the diagram for this problem. If it were taken off the vertical, then it would be just that. Taken from a line that is straight up instead of lying down.

OMG thanks soo much! At least I got one right! Okay next question, is 1 gonna be a right angle?? & How can you tell if its right angled or not?

 

[sophia_xo]

HELLO anyone around I need help TONIGHT!!!

A ship is tied to a dock with a rope length 10m. At low tide, the rope is stretched tight forming an angle of 30 degrees with the horizontal. At high tide, the stretched rope makes an angle of 45 degrees with the horizontal. How much closer to the dock, horizontally, is the ship at high tide than at low tide? Determine an exact expression. Then use a calculator to determine an approximate answer, correct to the nearest tenth of a metre.

** DIAGRAM REQUIRED

 

[BigGlenntheHeavy]

\(\displaystyle sophia\_xo, \ anyone \ can \ solve \ equations \ through \ practice, \ but \ in \ real \ life \ we \ usually \ have \ to \ do\)

\(\displaystyle \ with \ "word \ problems".\)

\(\displaystyle In \ the \ above \ "word \ problem", \ you \ have \ two \ right \ triangles, \ both \ with \ a \ hypotenuse \ of \ ten\)

\(\displaystyle meters, \ one \ triangle \ (low \ tide) \ with \ an \ angle \ of \ 30^0 \ coincidence \ with \ distance \ d_1 \ and\)

\(\displaystyle the \ other \ triangle \ (high \ tide) \ with \ an \ angle \ of \ 45^0 \ coincidence \ with \ distance \ d_2.\)

\(\displaystyle Hence, \ cos(30^0) \ = \ \frac{d_1}{10} \ and \ cos(45^0) \ = \ \frac{d_2}{10}, \ solve \ each \ for \ d \ and \ you \ are \ done.\)

 

[galactus]

#6:

Again the law of cosines comes into play to find the distance between the towns.

Distance from Haytown to Beeville: \(\displaystyle \sqrt{64+100-2(8)(10)cos(80)}\)

Now, the helicopter is halfway between them and 1000 feet up. Use the info to find the angle of elevation.

The angle of elevation is the angle you have to look up from the horizon to see the helicopter. I have attached a rather sloppy Paint diagram, but hopefully it gives the idea. My dashed lines are a little crooked

You know the helipcopter is 1000 feet in the air. Find the distance from the boat to the shore directly under the helipcopter. Then, use the law of tangents to find the angle of elevation.

 

[anksanpara]

S1 & S2 REPRESENTTHE POSITION OF SHIP AT LOW AND HIGH TIDE RESPECTIVELY.
LET THE DISTANCE FROM DOCK BE b AND a RESPECTIVELY.
cos 30 =b/10 => b=5sqroot3
cos 45=a/10 => a=5sqroot2

required is (b-a) ie 5 ( root 3-root2)=5(1.73205 08075-1.41421 35623)=1.589186226 metres