Trigonometric form
- Thread starter baha jaff
- Start date
write the complex number in the trigonometric form whereis real number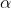

Write the complex number in the trigonometric form whereis real number.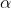
. . \(\displaystyle \dfrac{\cos\alpha + i\sin\alpha}{\cos\alpha - i\sin\alpha}\)
