You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Values of r and h (don't know they are estimated)
- Thread starter kinfo
- Start date
D
Deleted member 4993
Guest
Drop perpendiculars from the end-point of those sticks - to the x-y plane and z-axis. (edited)Hello all
I have a problem, being a part of big task.
Solution exists. But i don't know how it was found.
Can you explain me?
Thx!
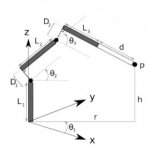
Picture and formulas have attached:
h = L1+ L2*sinθ2+D1*cosθ2+(L3+d)*sin(θ2+θ3)+D2*sin(θ2+θ3)
r = L2*cosθ2 - D1*sinθ2+(L3+d)*cos(θ2+θ3)-D2*sin(θ2+θ3)
View attachment 8945
Now look at the drawing again - the method should jump-out at you.
If you still cannot figure it out post the drawing again with those perpendiculars drawn in there. We will continue from there.
Last edited by a moderator:
Drop perpendiculars from the end-point of those sticks - to the x-axis and z-axis.
Now look at the drawing again - the method should jump-out at you.
If you still cannot figure it out post the drawing again with those perpendiculars drawn in there. We will continue from there.
Sorry, perpendiculars aren't incitements for me, sorry.
D
Deleted member 4993
Guest
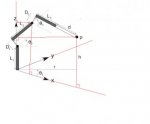
Those perpendiculars will meet the line "r".Sorry, perpendiculars aren't incitements for me, sorry.Let's continue from here ...
View attachment 8947
Label those points of intersections.
There should be another perpendicular to thr left of the z-axis and down to the x-y plane. Label the point of intersection of that perpendicular with line segment ("r" extended)
Those perpendiculars will meet the line "r".
Label those points of intersections.
There should be another perpendicular to thr left of the z-axis and down to the x-y plane. Label the point of intersection of that perpendicular with line segment ("r" extended)
Sorry for my problems with geometry, i know, that it is a shame
is new pic a right one?
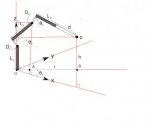
Hello, do we suppress our collaboration?